Abstract¶
We consider dynamic stair climbing with the HRP-4 humanoid robot as part of an Airbus manufacturing use-case demonstrator. We share experimental knowledge gathered so as to achieve this task, which HRP-4 had never been challenged to before. In particular, we extend walking stabilization based on linear inverted pendulum tracking by quadratic programming-based wrench distribution and a whole-body admittance controller that applies both end-effector and CoM strategies. While existing stabilizers tend to use either one or the other, our experience suggests that the combination of these two approaches improves tracking performance. We demonstrate this solution in an on-site experiment where HRP-4 climbs an industrial staircase with 18.5 cm high steps, and release our walking controller as open source software.
Content¶
The paper on HAL is a post-print I have kept updating after the conference to keep up with the later additions and fixes implemented in the walking controller. See the release notes on GitHub for an overview of the major changes since the conference version (v1.1).
Supplementary material¶
| Controller documentation | |
| Floating base observer used in this controller | |
| Overview of the controller's principles | |
| Python prototype of the walking trajectory generator | |
| Tuning the stabilizer of the controller |
BibTeX¶
@inproceedings{caron2019icra,
title = {Stair Climbing Stabilization of the {HRP}-4 Humanoid Robot using Whole-body Admittance Control},
author = {Caron, St{\'e}phane and Kheddar, Abderrahmane and Tempier, Olivier},
booktitle = {IEEE International Conference on Robotics and Automation},
url = {https://hal.archives-ouvertes.fr/hal-01875387},
year = {2019},
month = may,
doi = {10.1109/ICRA.2019.8794348},
}
Discussion ¶
You can subscribe to this Discussion's atom feed to stay tuned.
-

Reader #1
Posted on
Ankle angular velocities are clamped in the foot damping controller. How significant is this? Does the pipeline rely on this?
-

Stéphane
Posted on
We clamped angular velocities at 0.2 rad/s for the ankles. In the nominal behavior (a.k.a. "if everything goes well"™) no clamping should happen, so the control pipeline does not rely on this part. This clamping is rather a safety to avoid some states going from bad to worse: if the ZMP hits the boundary of its support area and the foot starts to tilt around its edge, force/torque sensors may measure an obscenely-far ZMP. We don't want to forward this value unclamped to a direct velocity controller ;-)
-
-

Reader #2
Posted on
In the MPC trajectory generator, what ZMP constraints are enforced during double support?
-

Stéphane
Posted on
To compute open-loop walking trajectories (i.e. before sensor readings and DCM feedback, which are the task of the stabilizer), we solve linear model predictive control (MPC) quadratic programs. These programs follow the formulation from Wieber et al., see e.g. the writeup in Brasseur et al. (2015). In particular, problems from this line of work use CoM jerk as control inputs/optimization variables, and don't have inequality constraints during double support phases, owing to the fact that these phases are no more than one or two timesteps. See the ZMP inequality constraint FAQ of the controller for more technical details.
-
-

Reader #3
Posted on
Why isn't there an angular momentum task in whole body control?
-

Stéphane
Posted on
Although the linear inverted pendulum model assumes constant angular momentum around the CoM, this controller does not try to explicitly control angular momentum. Rather, it relies on chest posture control for the upper body, and treats angular momentum variations as unmodeled disturbances handled after the fact by DCM feedback. Chest posture control is synchronized with foot damping control to adapt to terrain variations: see the angular momentum task FAQ of the controller for more technical details.
-
-

Reader #4
Posted on
What are the pros and cons of CoM admittance control?
-

Stéphane
Posted on
While we used CoM admittance control in 2019 stair climbing experiments, such as the one you see in the video above, we disabled it by default when distributing the open source controller. This choice is detailed in the CoM admittance control FAQ of the controller. In short: it improves disturbance rejection when contact force constraints are saturated (like we had when stepping up), but on stiff position-controlled robots like HRP-4 it has a tendency to pick up resonance vibrations.
-
-

Reader #5
Posted on
How is the divergent component of motion estimated?
-

Stéphane
Posted on
As now described in Appendix B, we compute the translation and orientation of the floating base using the classical IMU with anchor frame estimate. We then derive the CoM position by combining it with joint encoder measurements, and the CoM velocity by first-order low-pass filtering of this position.
-
-

Reader #6
Posted on
Why use damping control at the foot contact frame rather than, say, an acceleration-based force control law?
-

Stéphane
Posted on
The answer can be found in Equation (2) of Kajita et al. (2001). Robots from the HRP series have inherited from their Honda elders the choice of a mechanical flexibility (rubber bushes and linear dampers) added between the ankle and foot links. Stiffness dominates damping in this flexibility, that is, in practice where is a contact frame angle. We then use as a ground reaction torque model:
Usually the environment is static, so that the time-derivative of this expression is:
Foot damping control corresponds to the following angular velocity:
In closed loop, this yields:
This ensures that as .
-

Reader #6
Posted on
OK, but why in practice use damping control rather than an acceleration-based formulation?
-

Stéphane
Posted on
Large stiffness and low damping were rather a design choice that came with the robots we worked with. The second-order model with both stiffness and damping coefficients has more parameters to tune, but if this more complex model will anyway behave like a first-order model. Let us apply Occam's razor then: using the first-order model, we get similar performance with less parameters to tune and simpler code to maintain 😉
-
-
-
-

Reader #7
Posted on
Shall we try moving away from such high-stiffness low-damping at the contact interface?
-

Stéphane
Posted on
Absolutely, moving away from high stiffness and low damping at contact makes sense in my opinion. We tried moving away from this setting when walking on gravel with soft soles: the soles had a Young's modulus of 0.32 MPa (versus 5 MPa in previous works and I-don't-know-how-much for the default hard robot soles) meaning we reduced rather than increase . We still walked on hard floor though. There were two takeaway observations from this work:
First, the interaction with the ground through soft soles had more (ankle displacement to reaction force change) delay, i.e. lower force control bandwidth. This is not great for balance control where, when the stabilizer outputs a desired contact wrench, we want this wrench to be applied to the environment as fast as possible. That's one thing to look at: what combinations of and maximize the force control bandwidth?
Second, foot impacts at touchdown with soft soles were better mitigated mechanically. Walking controllers typically touch down earlier than expected at every step, which incurs undesired CoM velocity disturbances (foot impacts after they propagate across the kinematic chain). But with the soft soles these impacts were lower. If we imagine a function at touchdown, it is likely decreasing in yet increasing in . This leads us to another question: for a given (and some model of early-touchdown impact), what values of minimize ?
-
-

Reader #8
Posted on
What is the formula for the matrix in Equation (10)?
-

Stéphane
Posted on
This matrix is given by:
with the friction coefficient, the half-length and the half-width of the rectangular contact area. Check out this paper for the derivation of this formula, which corresponds to its equations (15) to (20). In code, it is implemented in the functions:
- Contact.wrench_inequalities() of pymanoid (Python)
- Stabilizer::wrenchFaceMatrix() of the lipm_walking_controller (C++)
-
-

Seung Hyeon Bang
Posted on
I have a question regarding the ankle torque minimization (Eq. (13)) in II-C, Contact Wrench Distribution. What is the benefit of minimizing ankle torque (Eq. (13)) over minimizing the contact wrench in each sole center frame (${}{lc} W$, )?
I believe the position of the sole center frame is in the bottom center of the foot, which directly contacts with the ground, while the ankle frame is located in the same planar surface offset along and axes of the sole center frame, based on the discussion in lipm_walking_controller#69.
-

Stéphane
Posted on
Ankle torque minimization is motivated by the design of the soles of HRP robots, which is inherited from Honda's humanoid robot design:
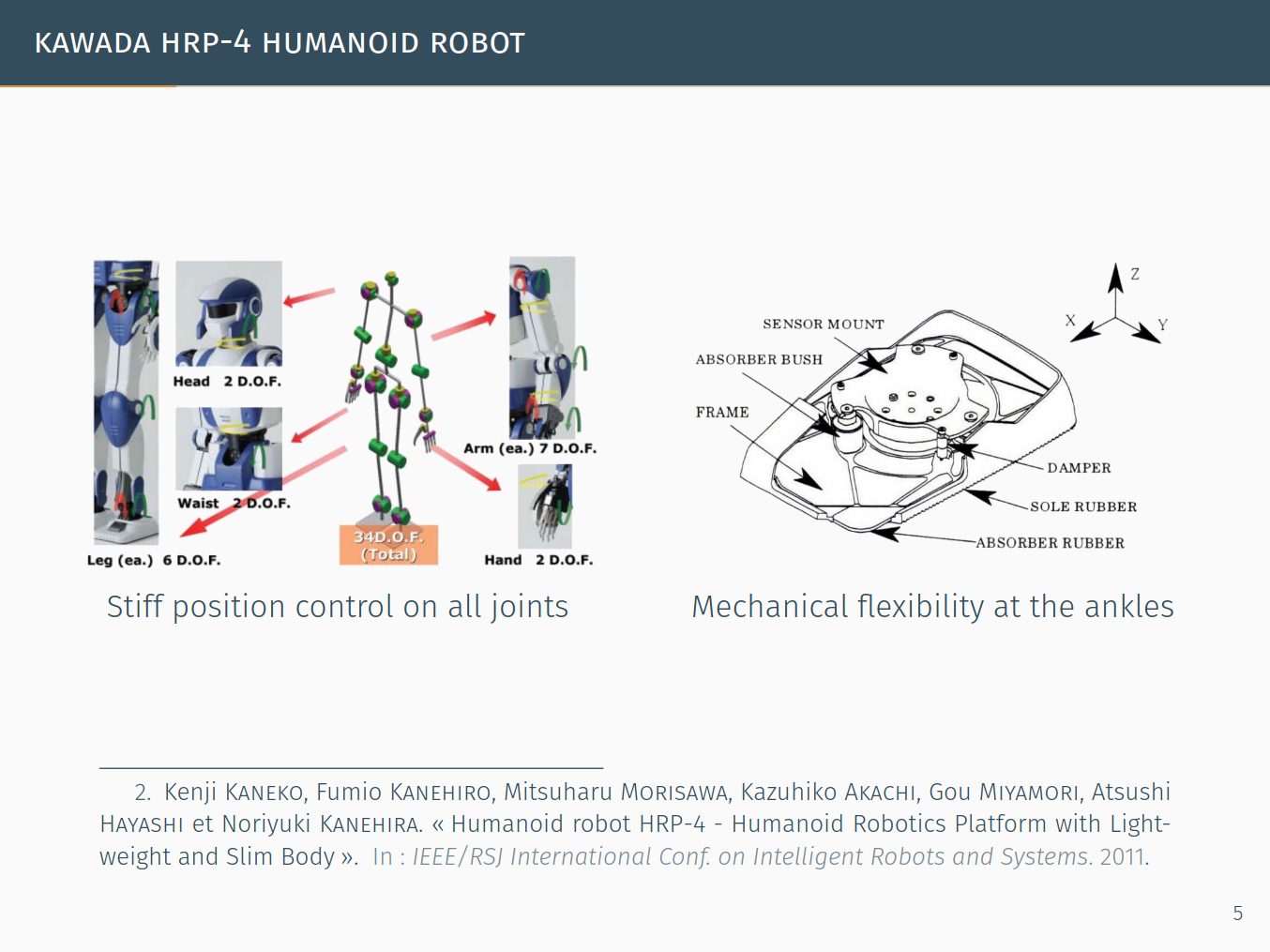
(Source: slides 4 and 5 in this presentation.)
The mechanical flexibility below the ankles is here to reduce the rigidity of the contact interaction with the environment. This means protecting the force sensor from hard impacts, but also importantly reducing the control frequency required for foot admittance control.
One downside of this flexibility is that our sensing and admittance control laws are based on the assumption that its deflection is small. (To be precise, this deflection is the orientation of the sole frame with respect to the ankle frame.) The larger the deflection, the worse our control becomes. That's why most works dealing with HRP robots try to keep this deflection small.
Keeping the flexibility deflection small is the motivation behind deflection observers like SpringEstimator. In this controller, we assume that there exists a linear underlying model: and minimize the ankle torque as a proxy to keep the deflection low.
-
-

Seung Hyeon Bang
Posted on
Looking at the lipm_walking_controller/src/Stabilizer.cpp, I wonder why you weighted more on
tauxandtauy. Is this because you don't want to generate tilting motions in the x and y local ankle frame (by minimizing the external wrench applied on the ankle joint through Eq. (13), you would expect the ankle joint to execute small torque command)?-

Stéphane
Posted on
The coordinates , more precisely: "the moment of ground contact forces around the local and axes of the projected ankle frame", correspond to the center of pressure (CoP) via the cross-product formula:
where is the normal vector of the projected ankle frame (orthogonal to the sole surface). The motivation for weighing those two coordinates more than the third one is to give priority to CoP control over yaw-moment control. There are at least two reasons why this is a good idea:
- Centers of pressure under each contact contribute directly to the net ZMP, which is what we aim to regulate down the line.
- Centers of pressure contribute indirectly to the yaw-moment friction condition:
where is the distance between the CoP and the edge of the contact surface, which we try to keep as large as possible (by minimizing ankle torques, i.e. keeping each CoP at the origin of its corresponding projected ankle frame). The larger is, the less the robot has to pay attention to as yaw slippage becomes less likely.
-
-

Seung Hyeon Bang
Posted on
In the paper, you stated:
From eq. (4), it can be implemented indifferently by adding or substracting to the commanded . We choose the latter in what follows.
instead of adding DCM velocity feedback to damp potential oscillations. Could you tell me the reason why you chose the ZMP feedback instead of DCM velocity feedback to get the commanded ZMP law (equation before Eq.(9)) in the paper?
-

Stéphane
Posted on
The post-print is actually out-of-phase with the code on this point: in lipm_walking_controller#16 we switched from ZMP to DCM derivative error. As far as I remember the motivation for it was to be able to do pole placement lipm_walking_controller#22, where the DCM derivative term is better decoupled from the proportional and integral ones than the previous ZMP term.
-
-

Seung Hyeon Bang
Posted on
In the case that the robot does not have an F/T sensor to measure the ZMP, do you think it is possible to use the DCM velocity feedback law to get the commanded ZMP (eventually net contact wrench)?
-

Stéphane
Posted on
If the robot does not have F/T sensors a big question will be: how does it implement its force control?
The DCM velocity error appears in the DCM feedback loop, the one that converts DCM tracking errors to a commanded ZMP. The point is then that, at the next stage, this commanded ZMP should be compared against a "measured ZMP". If the measured ZMP is observed by e.g. finite differentiation of the measured DCM, I would be concerned that it suffers from a lot of noise and delay. But I haven't tried this directly, so it's worth checking on a real robot 😉
-
Feel free to post a comment by e-mail using the form below. Your e-mail address will not be disclosed.