In robotics, the Zero-tilting Moment Point (ZMP) is a characteristic point
used notably in legged locomotion. Informally, and under some assumptions we
will see below, it represents the point where the resultant of reaction forces
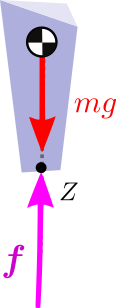
from a contact act on a system. For instance, the rigid body depicted in the
neighboring figure is in static equilibrium if and only if its ZMP is at the
vertical of its center of mass.
Definition
Formally, the ZMP refers to the set of points in space that cancel the moment
of contact forces with respect to a plane (typically, the ground plane). This
set is actually an axis, not a point , but for starters, let
us follow the traditional derivation where the ZMP on the ground plane. This
derivation starts with the Newton-Euler equations of motion of any multi-body system:
m p ¨ G = m g + f c L ˙ O = O G → × m g + τ G c \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
m \bfpdd_G & = m \bfg + \bff^c \\
\dot{L}_O & = \overrightarrow{OG} \times m \bfg + \bftau^{c}_G
\end{align*} m p ¨ G L ˙ O = m g + f c = OG × m g + τ G c where m \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
m m g \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfg g G \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
G G p ¨ G \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfpdd_G p ¨ G L ˙ O \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\dot{L}_O L ˙ O O \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
O O w G c = [ τ G c f c ] ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw^c_G =
[\bftau^c_G\ \bff^c]) w G c = [ τ G c f c ]) net contact wrench, that is, the sum of
all contact wrenches exerted onto the robot, with coordinates taken at the
center of mass (COM) G \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
G G
Define the gravito-inertial wrench of the multi-body system, which only depends
on its accelerations:
f g i = d e f m ( g − p ¨ G ) τ O g i = d e f O G → × m g − L ˙ O \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bff^{gi} & \defeq m (\bfg - \bfpdd_G) \\
\bftau^{gi}_O & \defeq \overrightarrow{OG} \times m \bfg - \dot{L}_O
\end{align*} f g i τ O g i = def m ( g − p ¨ G ) = def OG × m g − L ˙ O Newton-Euler equations can then be written in wrench form using screw algebra : w g i + w c = 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw^{gi} + \bfw^{c} = \boldsymbol{0} w g i + w c = 0 Z \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
Z Z
τ Z g i × n = 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bftau^{gi}_Z \times \bfn = \boldsymbol{0} τ Z g i × n = 0 where n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfn n
τ Z g i × n = ( τ O g i + Z O → × f g i ) × n = τ O g i × n + ( Z O → ⋅ n ) f g i − ( f g i ⋅ n ) Z O → \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bftau^{gi}_Z \times \bfn & = (\bftau^{gi}_O + \overrightarrow{ZO} \times \bff^{gi}) \times \bfn \\
& = \bftau^{gi}_O \times \bfn + (\overrightarrow{ZO} \cdot \bfn) \bff^{gi} - (\bff^{gi} \cdot \bfn) \overrightarrow{ZO}
\end{align*} τ Z g i × n = ( τ O g i + ZO × f g i ) × n = τ O g i × n + ( ZO ⋅ n ) f g i − ( f g i ⋅ n ) ZO by developping the vector triple product . Let us
suppose for now that O \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
O O Z \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
Z Z n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfn n Z O → ⋅ n = 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\overrightarrow{ZO} \cdot \bfn = 0 ZO ⋅ n = 0
O Z → = n × τ O g i f g i ⋅ n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
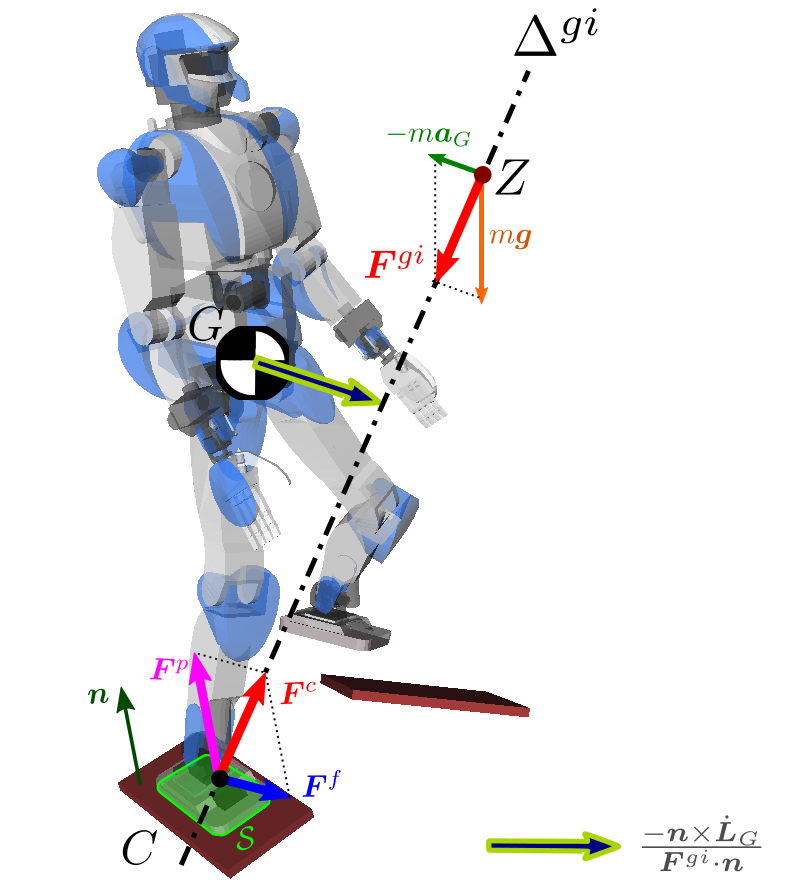
\overrightarrow{OZ} = \frac{\bfn \times \bftau^{gi}_O}{\bff^{gi} \cdot \bfn} OZ = f g i ⋅ n n × τ O g i This formula is used in practice to compute the ZMP from force sensors or from an inertial measurement
unit , which are
usually embedded in current legged robots. ZMPs can also be called zero moment
points for short in some contexts, for example in legged locomotion when the
angular momentum is kept constant at the center of mass so that τ Z g i = τ G g i = 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bftau^{gi}_Z
= \bftau^{gi}_G = \bfzero τ Z g i = τ G g i = 0
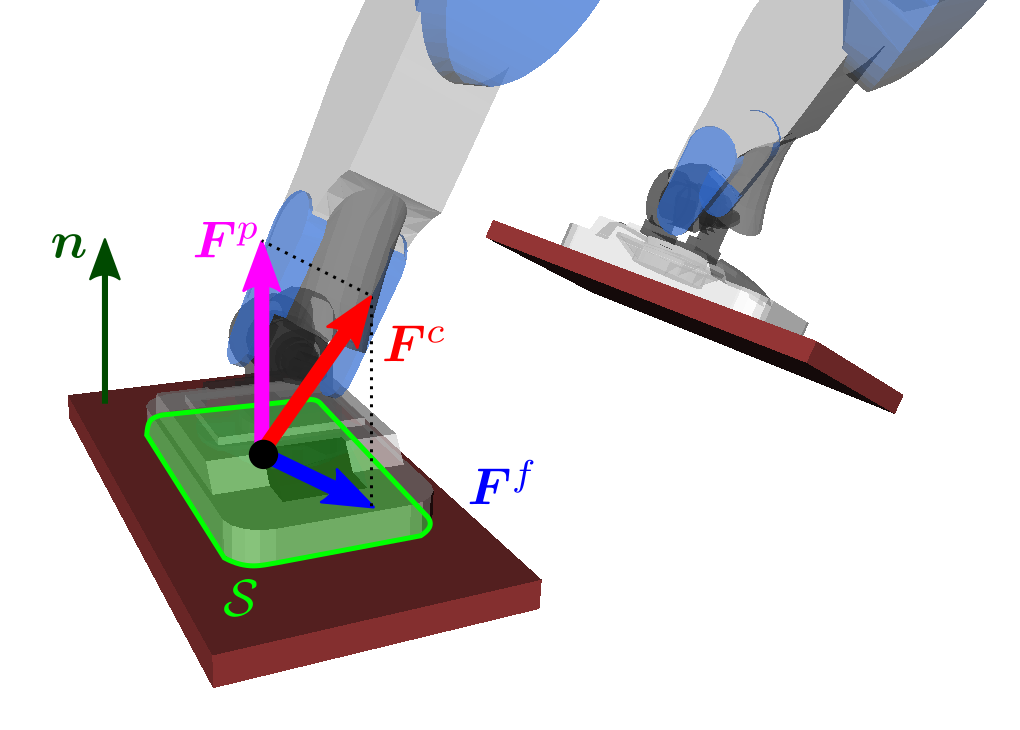
Center of pressure
The center of pressure (COP) is a dynamic point defined in between two bodies
in contact. Unlike the ZMP, which we defined from the accelerations of the
multi-body system, the COP is a local quantity defined from interaction forces
at the contact surface. These two different approaches yield the same point
when the robot is in single-contact with its environment, or walks on a flat
floor (Sardain and Bessonnet, 2004) .
Let us consider the case where a foot of the robot contacts a plane surface:
The resultant f c \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^c f c
the resultant pressure force f p = ( f c ⋅ n ) n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^p = (\bff^c \cdot \bfn) \bfn f p = ( f c ⋅ n ) n
the resultant friction force f f = f c − f p \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^f = \bff^c - \bff^p f f = f c − f p ( f f ⋅ n = 0 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
(\bff^f \cdot \bfn = 0) ( f f ⋅ n = 0 )
These two forces are the sum of infinitesimal forces applied through all
elements d S \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{\rm d}\mathcal{S} d S S \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{S} S p ( P ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
p(P) p ( P ) P ∈ S \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
P \in \mathcal{S} P ∈ S
f p = ∫ P ∈ S p ( P ) n d S \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^p = \int_{P \in \mathcal{S}} p(P) \bfn {\rm d}\mathcal{S} f p = ∫ P ∈ S p ( P ) n d S Pressure is always a positive quantity since the foot cannot penetrate the
ground surface. As a consequence, there always exists a center of pressure
C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
C C f p \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^p f p C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
C C
τ C p = 0 O C → × ( f p ⋅ n ) n = − τ O p ( f p ⋅ n ) n × O C → × n = − n × τ O p \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bftau^p_C & = \boldsymbol{0} \\
\overrightarrow{OC} \times (\bff^p \cdot \bfn) \bfn & = - \bftau^p_O \\
(\bff^p \cdot \bfn)\,\bfn \times \overrightarrow{OC} \times \bfn & = -\bfn \times \bftau^p_O
\end{align*} τ C p OC × ( f p ⋅ n ) n ( f p ⋅ n ) n × OC × n = 0 = − τ O p = − n × τ O p As both points O \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
O O C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
C C n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfn n
O C → = τ O p × n n ⋅ f p \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\overrightarrow{OC} = \frac{\bftau^p_O \times \bfn}{\bfn \cdot \bff^p} OC = n ⋅ f p τ O p × n Meanwhile, friction forces are tangent to the contact surface, so that their
moment is aligned with n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfn n
O C → = τ O c × n n ⋅ f c \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\overrightarrow{OC} = \frac{\bftau^c_O \times \bfn}{\bfn \cdot \bff^c} OC = n ⋅ f c τ O c × n Where we recognize the same formula as the one used to define the ZMP, except
that it is now applied to the (local) contact wrench rather than the (global)
gravito-inertial wrench. Now, remember how w g i = − w c \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw^{gi} = -\bfw^c w g i = − w c (Sardain et Bessonnet, 2004) .
The figure above represents the COM G \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
G G C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
C C Z \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
Z Z Δ g i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\Delta^{gi} Δ g i G \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
G G ( L ˙ G = 0 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
(\dot{L}_G = \boldsymbol{0}) ( L ˙ G = 0 ) (Kajita et Tani, 1991) .
Support area
As long as the contact is maintained, the COP will lie inside the contact
surface S \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{S} S
τ O c = ∫ P ∈ S O P → × p ( P ) n d S \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bftau^c_O = \int_{P \in {\mathcal{S}}} \overrightarrow{OP} \times p(P) \bfn
{\rm d}{\mathcal{S}} τ O c = ∫ P ∈ S OP × p ( P ) n d S So that the COP formula above becomes:
O C → = ∫ P ∈ S p ( P ) O P → d S ∫ P ∈ S p ( P ) d S \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\overrightarrow{OC} = \frac{\int_{P \in {\mathcal{S}}}
p(P)\,\overrightarrow{OP}\,{\rm d}{\mathcal{S}}}{\int_{P \in {\mathcal{S}}} p(P) {\rm
d}{\mathcal{S}}} OC = ∫ P ∈ S p ( P ) d S ∫ P ∈ S p ( P ) OP d S Thus, the COP can be seen as the average of ground contact points weighted
by their respective pressures. When it crosses the boundaries of S \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{S} S S \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{S} S C ∈ S \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
C \in \mathcal{S} C ∈ S non-tilting contact condition.
To go further
Although it has been applied to balancing legged robots, the zero-tilting
moment point is more generally a characteristic point of any wrench. In
balancing, we usually control the ZMP of the net contact wrench, which can be
derived even in the presence of external forces . You can check out how the ZMP of a
humanoid controller behaves using this Docker image to build up your intuition.
ZMP support areas can be extended to multi-contact scenarios , that is, to settings where feet or
hand contacts are made with different non-coplanar surfaces. However, their 2D
nature makes them a little restrictive for multi-contact locomotion. In a later
walking trajectory generator, they were therefore extended to the 3D cone of
COM accelerations .
Discussion
You can subscribe to this Discussion's atom feed to stay tuned.
Feel free to post a comment by e-mail using the form below. Your e-mail address will not be disclosed.