Quadratic programming in Python

Standard form of quadratic programs¶

A quadratic program (QP) is written in standard form as:

Here $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x$ is the vector of optimization variables $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x_1, \ldots, x_n$. The matrix $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} P$ and vector $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} q$ are used to define a general quadratic objective function on these variables, while the matrix-vector pairs $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} (G, h)$ and $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} (A, b)$ respectively define inequality and equality constraints. Vector inequalities apply coordinate by coordinate, so that for instance $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x \geq 0$ means that every coordinate of the vector $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x$ is positive.

This mathematical formulation means that a QP finds the minimum of a quadratic function over a linear set:

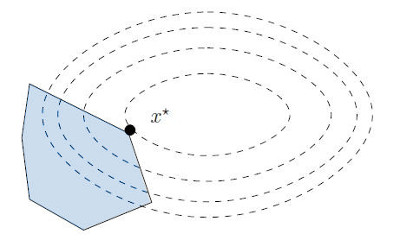
In the 2D illustration above, the level sets of the quadratic function are drawn as dashed ellipses while the linear set of inequality constraints corresponds to the blue polygon. (The description of a polygon, or more generally a polyhedron, by linear inequality constraints is called the halfspace representation.) Since the global optimal of the objective function is outside of the polygon, the solution $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x^*$ of the QP lies on the boundary of this polygon. The set of linear constraints that are saturated at $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x^*$ is called the active set, but that's a story for another post...

Back to the standard form, you will notice that there is no constant term in the objective function. Indeed, it would have no effect on the result of the optimization, which is the location of the solution $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x^*$. For example, the quadratic expression $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} \| A x - b \|^2$ of a least squares optimization is written in standard form with $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} P = 2 A^T A$ and $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} q = -2 A^T b$ (see the example below for a small proof of this).

The standard form also assumes, without loss of generality, that the matrix $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} P$ is symmetric. Any matrix $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} M$ can be decomposed as sum of its symmetric part $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} M^+$ and antisymmetric part $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} M^-$, and the latter yields zero in $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x^T M^- x$. Note that some solvers (like CVXOPT) assume that you provide a symmetric cost matrix right away: they won't check this, and will return wrong results if you don't.

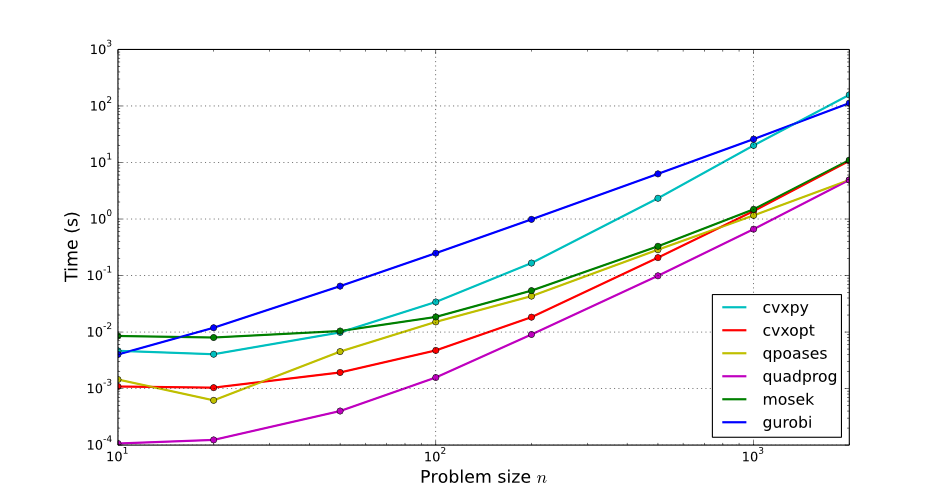
Setting up QP solvers¶

Two readily-available QP solvers in Python are CVXOPT and quadprog. They can be installed by:

$ sudo CVXOPT_BUILD_GLPK=1 pip install cvxopt
$ sudo pip install quadprog

CVXOPT uses its own matrix type, and it requires the matrix $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} P$ of the objective function to be symmetric. To be on the safe side, you can wrap it as follows:

def cvxopt_solve_qp(P, q, G, h, A=None, b=None):
    P = .5 * (P + P.T)  # make sure P is symmetric
    args = [cvxopt.matrix(P), cvxopt.matrix(q)]
    args.extend([cvxopt.matrix(G), cvxopt.matrix(h)])
    if A is not None:
        args.extend([cvxopt.matrix(A), cvxopt.matrix(b)])
    sol = cvxopt.solvers.qp(*args)
    if 'optimal' not in sol['status']:
        return None
    return numpy.array(sol['x']).reshape((P.shape[1],))

The quadprog module works directly on NumPy arrays so there is no need for type conversion. Its matrix representation is equivalent to the standard form but combines inequalities and equalities in a single matrix-vector pair:

def quadprog_solve_qp(P, q, G, h, A=None, b=None):
    qp_G = .5 * (P + P.T)   # make sure P is symmetric
    qp_a = -q
    if A is not None:
        qp_C = -numpy.vstack([A, G]).T
        qp_b = -numpy.hstack([b, h])
        meq = A.shape[0]
    else:  # no equality constraint
        qp_C = -G.T
        qp_b = -h
        meq = 0
    return quadprog.solve_qp(qp_G, qp_a, qp_C, qp_b, meq)[0]

In these two functions we assume that the QP has inequality constraints. For more general functions that handle all combinations of inequality, equality and box-inequality constraints $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} lb \leq x \leq ub$, or if you want to try out other solvers, you will find a unified solve_qp function with a solver keyword argument in the qpsolvers library.

Example of a linear least squares problem¶

For a small example, let us see how to solve:

This problem is in linear least squares form. Denoting its cost function by $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} \| M x - b\|^2$, we can convert it to QP form as follows:

Multiplying by a positive constant $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} (1/2)$ does not change the value of the optimum $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x^*$. Similarly, the constant offset $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} b^T b$ does not affect $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x^*$, therefore we can leave it out. Meanwhile, $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} y^T = y$ for any real number $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} y$, therefore $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} x^T M^T b = b^T M x$ and we can combine the two middle terms into a single $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} q = -M^T b$. In Python, we then write:

M = array([[1., 2., 0.], [-8., 3., 2.], [0., 1., 1.]])
P = dot(M.T, M)
q = -dot(M.T, array([3., 2., 3.]))
G = array([[1., 2., 1.], [2., 0., 1.], [-1., 2., -1.]])
h = array([3., 2., -2.]).reshape((3,))

We can finally compute the solution to the least squares problem using either of our QP solvers:

In [1]: cvxopt_solve_qp(P, q, G, h)
Out[1]: array([ 0.12997347, -0.06498674,  1.74005305])

In [2]: quadprog_solve_qp(P, q, G, h)
Out[2]: array([ 0.12997347, -0.06498674,  1.74005305])

Comparing solver performances¶

In the following benchmark, I compared six different solvers. (Edit: this benchmark is severely outdated, check out qpbenchmark for a 2022 refresher.) Three of them are numerical, which is the approach we have seen so far:

• CVXOPT
• qpOASES
• quadprog (the Python module, which is not the same as QuadProg++)

The three others are symbolic, meaning that if you dig into their API they allow you to construct your problem formally (with variable names) rather than using the matrix-vector representation. This is convenient for big sparse problems, but slower and small problems such as the one we are looking at here. The three symbolic frameworks I tested are:

• CVXPY (using ECOS as the underlying solver)
• Gurobi
• MOSEK (wrapped by CVXOPT)

Note that ECOS and MOSEK are actually SOCP solvers, SOCP being a class of problems more general that QP. Here are sample computation times on my machine:

• qpOASES: 10000 loops, best of 3: 31.5 µs per loop
• quadprog: 10000 loops, best of 3: 34.1 µs per loop
• CVXOPT: 1000 loops, best of 3: 559 µs per loop
• Gurobi: 1000 loops, best of 3: 865 µs per loop
• CVXPY: 100 loops, best of 3: 2.81 ms per loop
• MOSEK: 100 loops, best of 3: 7.24 ms per loop

For further investigation, let us generate random problems of arbitrary size as follows:

def solve_random_qp(n, solver):
    M, b = random.random((n, n)), random.random(n)
    P, q = dot(M.T, M), dot(b, M).reshape((n,))
    G = toeplitz([1., 0., 0.] + [0.] * (n - 3), [1., 2., 3.] + [0.] * (n - 3))
    h = ones(n)
    return solve_qp(P, q, G, h, solver=solver)

The Toeplitz matrix used to generate inequalities is just an upper-tridiagonal matrix with coefficients 1, 2, 3, all other coefficients being zero. This matrix is sparse but represented by (dense) NumPy arrays here. Using the function above, I generated a benchmark for problem sizes ranging from 10 to 2,000, averaging computation times over 10 runs for each point. Here are the results:

The bottom line of this small comparison is that quadprog, which implements the Goldfarb-Idnani dual algorithm, simply rocks on well-conditioned dense problems. More generally, active-set solvers (quadprog and qpOASES here) perform best on dense problems. To see the benefit of interior-point solvers like Gurobi or MOSEK, one would have to use sparse matrix representation, which I didn't do in this example. (Edit: it has been done since then in qpsolvers.) Also, the performance of CVXPY here does not illustrate that of its underlying solver (ECOS), as it turns out calling the solver directly is much faster than going through CVXPY.

One last note on this benchmark is that all performances reported here are for cold start, that is to say, problems are solved from scratch every time without a good initial guess. One reason why qpOASES is a bit slow here is that it is designed (e.g. in terms of memory allocation) for solving series of QP problems that are close to each other, so that the solution to one can be used as initial guess to solve the next problem faster (this is known as warm starting). You might want to give qpOASES a closer look if you are in such scenarios.

To go further¶

You can run this benchmark on your own computer: the script was called benchmark_random_problems.py and located in the examples folder of the qpsolvers repository. Since the publication of this post, the library has grown to include more solvers (OSQP, qpSWIFT, SCS, ...) and features such as box inequalities.