In a previous post,
I compared the performances of two Linear Programming (LP) solvers, COIN and
GLPK, called by a Python library named PuLP. It then took around 100 ms to solve
problems of moderate size. As it turns out, this is way too slow for this
kind of problems, probably due to the fact that PuLP calls solvers externally
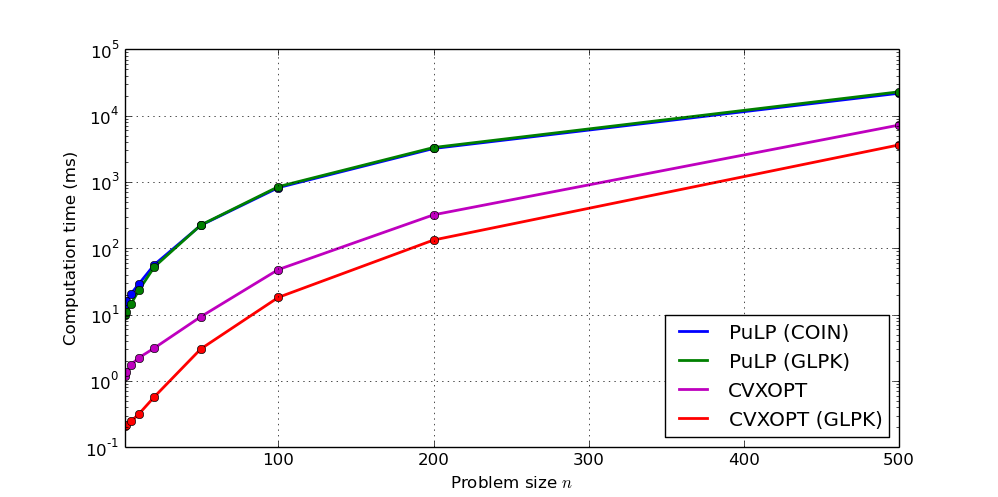
via the command line. In this second post, I used the CVXOPT library and compared the performances with the previous
approach. As it turns out, using CVXOPT is 50~70 times faster! Where it took
100 ms with PuLP, it now takes 2~3 ms with CVXOPT on my machine.
CVXOPT setup
If you don't plan on using external solvers such as GLPK or MOSEK, installing
CVXOPT on Ubuntu or Debian is as simple as:
$ sudo apt-get install python-cvxopt
To install GLPK as well, you'd best build from source. An easy way to get
everything done automatically is to use pip:
$ sudo apt-get install libglpk-dev
$ sudo CVXOPT_BUILD_GLPK=1 pip install cvxopt
You should now be able to import cvxopt from Python.
Matrix-vector LP problem
The problem for this benchmark is the same as in the previous post: find
a vector x∈[xmin,xmax]n that
minimizes the maximum of a set of affine functions:
minimizesubject tom∀i,ai+∑jbijxj≤m∀i,xmin≤xi≤xmaxHowever, from CVXOPT's documentation,
CVXOPT takes LP problems formulated as:
minimizesubject toc⊤xGx≤hAx=bWe thus need to formulate our problem in matrix-vector form. First, we append
m as the last coordinate of the variables vector x so
that m=c⊤x with c=[00…01]⊤. Next, we stack the scalars ai into a vector
a, and the vectors bi into a matrix B.
The LP problem becomes:
minimizes.t.c⊤xa+Bx≤0xmin≤x≤xmaxWhere the vector notation a≤b means ∀i,ai≤bi. Each instance of our benchmark problem is then a pair
(a,B) that we will generate by uniform random sampling in
[−1,1]n×[−1,1]n×n.
Solving LPs from CVXOPT
Here is the function that solves the LP corresponding to an instance
(a,B):
from numpy import array, eye, hstack, ones, vstack, zeros
def cvxopt_solve_minmax(n, a, B, x_min=-42, x_max=42, solver=None):
c = hstack([zeros(n), [1]])
# cvxopt constraint format: G * x <= h
# first, a + B * x[0:n] <= x[n]
G1 = zeros((n, n + 1))
G1[0:n, 0:n] = B
G1[:, n] = -ones(n)
h1 = -a
# then, x_min <= x <= x_max
x_min = x_min * ones(n)
x_max = x_max * ones(n)
G2 = vstack([
hstack([+eye(n), zeros((n, 1))]),
hstack([-eye(n), zeros((n, 1))])])
h2 = hstack([x_max, -x_min])
c = cvxopt.matrix(c)
G = cvxopt.matrix(vstack([G1, G2]))
h = cvxopt.matrix(hstack([h1, h2]))
sol = cvxopt.solvers.lp(c, G, h, solver=solver)
return array(sol['x']).reshape((n + 1,))
You can choose which solver to use via the solver keyword argument, for
example solver='glpk' to use GLPK. Leaving it to None will call
CVXOPT's default solver for Linear Cone Programs, which should be less
efficient than GLPK as it solves a more general class of problems.
Disabling the output from GLPK in CVXOPT
A minor problem I had was to disable solver outputs in CVXOPT. The standard way
to do that is via the options dictionary in cvxopt.solvers, which is
passed to the selected solver at instantiation time:
cvxopt.solvers.options['show_progress'] = False
It works for the default solver, but not with GLPK. A post on CVXOPT's bulletin
board points to the parameter LPX_K_MSGLEV, but it didn't work with my
version (1.1.7) of the software either. A docstring in the source code src/C/glpk.c
mentions another parameter msg_lev, which works for me:
cvxopt.solvers.options['glpk'] = {'msg_lev': 'GLP_MSG_OFF'} # cvxopt 1.1.8
cvxopt.solvers.options['msg_lev'] = 'GLP_MSG_OFF' # cvxopt 1.1.7
cvxopt.solvers.options['LPX_K_MSGLEV'] = 0 # previous versions
To go further
You can try out the lpsolvers
module to solve linear programs with CVXOPT or other solvers available in
Python.
Discussion
Feel free to post a comment by e-mail using the form below. Your e-mail address will not be disclosed.