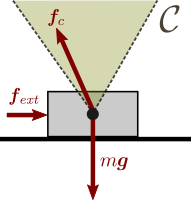
Consider the 2D example depicted in figure to the right. A 2D mass is in
contact with a single surface. This contact will remain fixed as long as the
contact force f c = m g − f e x t \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^c = m \bfg - \bff^{\mathit{ext}} f c = m g − f ext C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{C} C f c \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^c f c C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{C} C f c ∈ C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^c \in \mathcal{C} f c ∈ C ZMP support areas ) is of key interest as robots are
commonly controlled using only a small number of contact modes.
Coulomb friction
Consider the set of points { C i } \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\{C_i\} { C i } n i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfn_i n i C i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
C_i C i f i c \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^c_i f i c contact force
exerted at C i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
C_i C i
the normal component f i n = d e f ( n i ⋅ f i c ) n i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^n_i \defeq (\bfn_i \cdot \bff^c_i) \bfn_i f i n = def ( n i ⋅ f i c ) n i normal force , and
the tangential component f i t = d e f f i c − ( n i ⋅ f i c ) n i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^t_i \defeq \bff^c_i - (\bfn_i \cdot
\bff^c_i) \bfn_i f i t = def f i c − ( n i ⋅ f i c ) n i friction force at C i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
C_i C i
A point contact remains in the fixed contact mode while its contact
force f i c \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^c_i f i c friction cone directed by
n i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfn_i n i
( f i c ⋅ n i ) > 0 , and ∥ f i t ∥ 2 ≤ μ i ( f i c ⋅ n i ) , \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
(\bff^c_i \cdot \bfn_i) \ > \ 0, \quad
\textrm{and} \quad
\left\| \bff^t_i \right\|_2 \ \leq \ \mu_i (\bff^{c}_i \cdot \bfn_i), ( f i c ⋅ n i ) > 0 , and f i t 2 ≤ μ i ( f i c ⋅ n i ) , where μ i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mu_i μ i C i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
C_i C i ∥ ⋅ ∥ 2 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\| \cdot \|_2 ∥ ⋅ ∥ 2
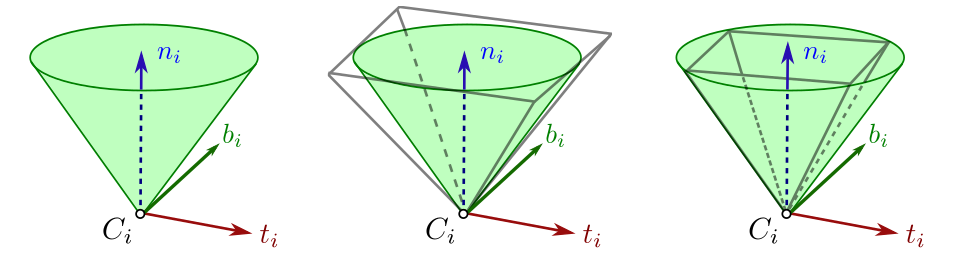
Linearized friction cones
A point contact remains in the fixed contact mode while its contact
force f i c \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^c_i f i c linearized friction cone
directed by n i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfn_i n i
f i c ⋅ n i > 0 , and f i t μ ~ i ( f i c ⋅ n i ) ∈ P n , \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bff^c_i \cdot \bfn_i \ > \ 0,
\quad \textrm{and} \quad
\frac{\bff^t_i}{\tilde{\mu}_i (\bff^{c}_i \cdot \bfn_i)} \ \in \ \mathcal{P}_n, f i c ⋅ n i > 0 , and μ ~ i ( f i c ⋅ n i ) f i t ∈ P n , where P n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{P}_n P n n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
n n
This approximation can be made as close as desired to the original model
by increasing the number of edges n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
n n P n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{P}_n P n n = 4 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
n=4 n = 4
f i c ⋅ n i > 0 ∣ f i c ⋅ t i ∣ ≤ μ ~ i ( f i c ⋅ n i ) , ∣ f i c ⋅ b i ∣ ≤ μ ~ i ( f i c ⋅ n i ) , \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bff^c_i \cdot \bfn_i & > 0 \\
| \bff^{c}_i \cdot \bft_i | & \leq \tilde{\mu}_i (\bff^{c}_i \cdot \bfn_i), \\
| \bff^{c}_i \cdot \bfb_i | & \leq \tilde{\mu}_i (\bff^{c}_i \cdot \bfn_i),
\end{align*} f i c ⋅ n i ∣ f i c ⋅ t i ∣ ∣ f i c ⋅ b i ∣ > 0 ≤ μ ~ i ( f i c ⋅ n i ) , ≤ μ ~ i ( f i c ⋅ n i ) , with ( t i , b i ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
(\bft_i, \bfb_i) ( t i , b i ) ( t i , b i , n i ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
(\bft_i, \bfb_i, \bfn_i) ( t i , b i , n i ) μ ~ i = μ i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\tilde{\mu}_i = \mu_i μ ~ i = μ i μ ~ i = μ i / 2 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\tilde{\mu}_i = \mu_i / \sqrt{2} μ ~ i = μ i / 2
Coulomb friction cone (left) with outer (middle) and inner (right) linear
approximations.
Discussion
You can subscribe to this Discussion's atom feed to stay tuned.
Feel free to post a comment by e-mail using the form below. Your e-mail address will not be disclosed.