What is a controller?

Robots run many layers of software. The layer that decides what actions to take based on the latest sensor readings is called the controller in control theory. In reinforcement learning, it is known as the agent.

Feedback loop¶

In the general sense, robot components can be classified in three categories: actuation (“the plant”, sometimes simply called “the robot”), sensing and control. A controller is, by definition,anything that turns robot outputs (a.k.a. “states”, for instance joint positions and velocities) into new robot inputs (a.k.a. “controls”, for instance joint accelerations or torques). Robot outputs are not known perfectly but measured by sensors. Putting these three components together yields the feedback loop:

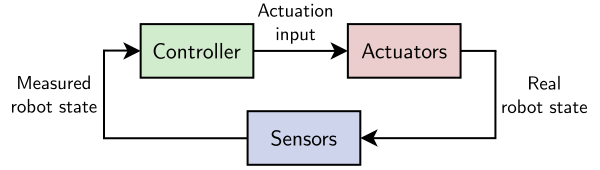
If we take the simple example of a velocity-controlled point mass, the input of your robot is a velocity and its output is a new position. A controller is then any piece of software that takes positions as inputs and outputs velocities. Under the hood, the controller may carry out various operations such as trajectory planning or PID feedback. For instance, a model predictive controller computes a desired future trajectory of the robot starting from its current (measured) state, then extracts the first controls from it and sends it to the robot.

Example of HRP-4¶

The HRP-4 humanoid robot from Kawada Industries is a position-controlled robot.

Inputs: desired joint positions
Outputs: joint angle positions, as well as the position and orientation of the robot with respect to the inertial frame (a.k.a. its floating base transform)

Being a mobile robot, it is underactuated, meaning its state has a higher dimension than its inputs. Measurements of the robot state are carried out by rotary encoders for joint angles and using an IMU for the free-flyer transform. A controller for HRP-4 therefore takes as inputs the robot’s state (joint positions + position and orientation with respect to the inertial frame) and outputs a new set of desired positions.

Terminology¶

Control theory has a bit more terminology to describe the feedback loop above. Here is the same loop with standard notations from this field:

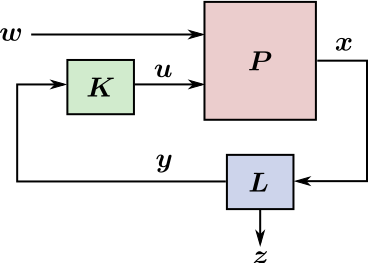
The real state $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfx$ of the system is an ideal quantity. Some components of it may not be observable by sensors, for example the yaw orientation of the robot with respect to gravity.

$\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfy$ is the output, the set of observable components in $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfx$ .
$\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfz$ is the exogenous output, the set of non-observable components in $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfx$ .
$\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfL$ is the state observer that estimates $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfy$ from available sensor readings.
$\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfK$ is the controller that computes the control input from the measured state.
$\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfu$ is the control input by which the controller can act on the plant.
$\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfP$ is the plant, the external system being controlled, a.k.a. the robot.
$\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfw$ is the exogenous input, a set of external causes unseen by the controller.

The vocabulary of control theory puts the plant-observer at the center, which is why $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfu$ is called the control input (although it's an output of the controller: because it's an input to the plant) and $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfy$ is called the output (it's an output of the observer and an input to the controller).

Exogenous inputs¶

Control theory precises the notion of exogenous inputs $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfw$ to represent external causes that the system cannot observe. For example, when a humanoid robot $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfP$ walking on unknown terrain is subjected to an external push $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfw$ , the robot cannot distinguish a terrain irregularity (there is a difference between the expected and measured contact forces caused by some unknown terrain shape) from the external push (the contact force difference is caused by the push). The push is then an exogenous input, required to integrate $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfP$ forward in time but unknown to the controller $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfK$ .

Reinforcement learning¶

Reinforcement learning frames the same problem with a different terminology. In reinforcement learning, $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfy$ is the observation, $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfu$ is the action, $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfP$ is the environment and $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfK$ is the agent. Most of the time, exogenous quantiies and the state observer $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfL$ are collectively included in $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfP$ , as reinforcement learning centers on the agent. The addition of reinforcement learning to classical control theory is a second input $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} r$ to the controller representing the reward obtained from executing action $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfu$ from state $\def\LdG{\dot{L}_G} \def\Ld{\dot{L}} \def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\calA{\mathcal{A}} \def\calB{\mathcal{B}} \def\calC{\mathcal{C}} \def\calD{\mathcal{D}} \def\calE{\mathcal{E}} \def\calF{\mathcal{F}} \def\calG{\mathcal{G}} \def\calH{\mathcal{H}} \def\calI{\mathcal{I}} \def\calJ{\mathcal{J}} \def\calK{\mathcal{K}} \def\calL{\mathcal{L}} \def\calM{\mathcal{M}} \def\calN{\mathcal{N}} \def\calO{\mathcal{O}} \def\calP{\mathcal{P}} \def\calQ{\mathcal{Q}} \def\calR{\mathcal{R}} \def\calS{\mathcal{S}} \def\calT{\mathcal{T}} \def\calU{\mathcal{U}} \def\calV{\mathcal{V}} \def\calW{\mathcal{W}} \def\calX{\mathcal{X}} \def\calY{\mathcal{Y}} \def\calZ{\mathcal{Z}} \def\d#1{{\rm d}{#1}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\dim{\rm dim} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xdd{\ddot{x}} \def\xd{\dot{x}} \def\ydd{\ddot{y}} \def\yd{\dot{y}} \def\zdd{\ddot{z}} \def\zd{\dot{z}} \bfx$ .

Q & A¶

How to achieve velocity/acceleration control on a position-controlled robot?

Sending successive joint angles along a trajectory with the desired velocities or accelerations, and relying and the robot’s stiff position tracking.

How to control the underactuated position of the robot in the inertial frame?

Using contacts with the environment and force control. For instance, position-controlled robots use admittance control to regulate forces at their end-effectors.

To go further¶

Many references explain clearly the terminology used in control theory. I liked Quang-Cuong Pham’s lecture notes on control theory. Richard Sutton's common model of the intelligent decision maker is a great step to unify the standpoints of control theory and reinforcement learning what those of other fields. Beyond what we've seen above, it introduces the concepts of transition model and value function as internal components of a general agent.

Discussion ¶

There are no comments yet. Feel free to leave a reply using the form below.