In inverse kinematics, our control problem is to bring task residuals , also known as task errors , to zero. If we denote by e ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfe(\bfq) e ( q ) q ∈ C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfq \in \mathcal{C} q ∈ C J ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ(\bfq) J ( q ) q ˙ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\qd q ˙
J ( q ) q ˙ = − α e ( q ) , α > 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ(\bfq) \qd = - \alpha \bfe(\bfq), \ \alpha > 0 J ( q ) q ˙ = − α e ( q ) , α > 0 In this post, we will clarify the definition of the Jacobian of a kinematic task, and see on a practical example why it matters to keep in mind this definition for 6D pose tasks.
Jacobian of a task
A kinematic task is fully defined by the residual function e ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfe(\bfq) e ( q )
J ( q ) : = ∂ e ∂ q ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ(\bfq) := \frac{\partial \bfe}{\partial \bfq}(\bfq) J ( q ) := ∂ q ∂ e ( q ) With this choice, the closed-loop behavior of integrating velocities q ˙ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\qd q ˙ J ( q ) q ˙ = e ˙ = − α e \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ(\bfq) \qd = \dot{\bfe} = - \alpha \bfe J ( q ) q ˙ = e ˙ = − α e e \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfe e α \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\alpha α
Jacobian of a position task
In this previous note , we considered the case of a position task, and defined its Jacobian as follows:
e p ( q ) = p − p ∗ J p ( q ) = ∂ p ∂ q ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bfe_p(\bfq) & = \bfp - \bfp^* \\
\bfJ_p(\bfq) & = \frac{\partial \bfp}{\partial \bfq}(\bfq)
\end{align*} e p ( q ) J p ( q ) = p − p ∗ = ∂ q ∂ p ( q ) This definition works because in this instance ∂ p ∂ q = ∂ e p ∂ q \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\frac{\partial \bfp}{\partial \bfq} = \frac{\partial \bfe_p}{\partial \bfq} ∂ q ∂ p = ∂ q ∂ e p not be the same as the Jacobian of the corresponding orientation or pose.
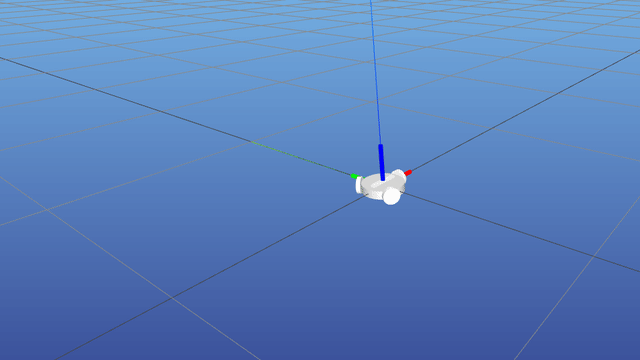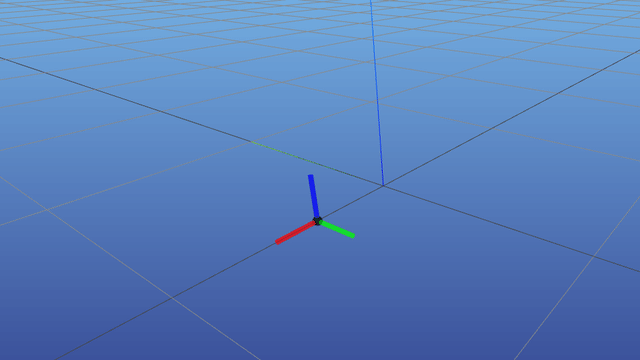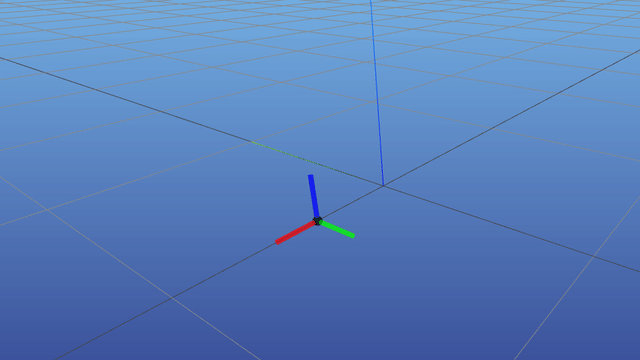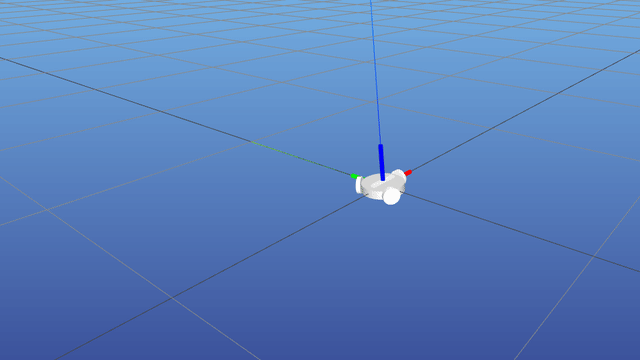
Pose task definition
Let us analyze the case of a pose task , where we control the pose T 0 b ∈ S E ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfT_{0b} \in SE(3) T 0 b ∈ SE ( 3 ) b \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
b b 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
0 0 t \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
t t T 0 t \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfT_{0t} T 0 t
Pose task residual
We can define the residual of our pose task as:
e ( q ) : = b ξ 0 b = T 0 t ⊖ T 0 b = log 6 ( T b 0 T 0 t ) = log 6 ( T b t ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfe(\bfq) := {}_b \bfxi_{0b} = \bfT_{0t} \ominus \bfT_{0b} = \log_6(\bfT_{b0} \bfT_{0t}) = \log_6(\bfT_{bt}) e ( q ) := b ξ 0 b = T 0 t ⊖ T 0 b = log 6 ( T b 0 T 0 t ) = log 6 ( T b t ) In this formula, the logarithm log 6 : S E ( 3 ) → s e ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\log_6 : SE(3) \to se(3) log 6 : SE ( 3 ) → se ( 3 ) S E ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
SE(3) SE ( 3 ) twists (elements of the corresponding Lie algebra s e ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
se(3) se ( 3 ) ⊖ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\ominus ⊖ micro Lie theory (MLT) writeup (equations (15) and (26)).
Formally, this residual is a function e : C → s e ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfe : \mathcal{C} \to se(3) e : C → se ( 3 ) C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{C} C s e ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
se(3) se ( 3 )
Frame Jacobian
The Jacobian of the pose of our frame, not to be confused with the Jacobian of the pose task, is:
b J 0 b ( q ) = ∂ T 0 b ∂ q ( q ) = lim τ → 0 T 0 b ( q ⊕ τ ) ⊖ T 0 b ( q ) τ = ∂ log 6 ( T b 0 ( q ) ⋅ ( T 0 b ( q ) ⋅ exp c ( τ ) ) ) ∂ τ ∣ τ = 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
{}_b \bfJ_{0b}(\bfq)
& = \frac{\partial \bfT_{0b}}{\partial \bfq}(\bfq) \\
& = \lim_{\bftau \to \bfzero} \frac{\bfT_{0b}(\bfq \oplus \bftau) \ominus \bfT_{0b}(\bfq)}{\bftau} \\
& = \left.\frac{\partial \log_6 (\bfT_{b0}(\bfq) \cdot (\bfT_{0b}(\bfq) \cdot \exp_{\mathcal{c}}(\bftau)))}{\partial \bftau} \right|_{\bftau=\bfzero}
\end{align*} b J 0 b ( q ) = ∂ q ∂ T 0 b ( q ) = τ → 0 lim τ T 0 b ( q ⊕ τ ) ⊖ T 0 b ( q ) = ∂ τ ∂ log 6 ( T b 0 ( q ) ⋅ ( T 0 b ( q ) ⋅ exp c ( τ ))) τ = 0 where ⊕ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\oplus ⊕ exp c : c → C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\exp_{\mathcal{c}} : \mathfrak{c} \to \mathcal{C} exp c : c → C τ = v δ t ∈ c \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bftau = \bfv \delta t \in \mathfrak{c} τ = v δ t ∈ c C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{C} C integrate (docs ) function of Pinocchio:
tau = velocity * dt
q * exp(tau) := integrate(model, q, tau)
To be consistent with our use of the right-minus in the residual, we use a right derivative, which is why b J 0 b \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}_b \bfJ_{0b} b J 0 b b \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
b b right Jacobian in micro-Lie terminology (MLT: equation (41a)). In practice we can compute it using the getFrameJacobian (docs ) function of Pinocchio, leaving the reference frame parameter to its default value (LOCAL).
Pose task Jacobian
The Jacobian of our pose task is defined by:
J ( q ) : = ∂ e ∂ q ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ(\bfq) := \frac{\partial \bfe}{\partial \bfq}(\bfq) J ( q ) := ∂ q ∂ e ( q ) The practical formula, which we will derive below, is:
J ( q ) = − Jlog 6 ( T t b ) b J 0 b ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ(\bfq) = -\text{Jlog}_6(\bfT_{tb}) {}_b \bfJ_{0b}(\bfq) J ( q ) = − Jlog 6 ( T t b ) b J 0 b ( q ) We see how, contrary to the position task, the Jacobian of the pose task is not the same as the frame Jacobian b J 0 b ( q ) . \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}_b \bfJ_{0b}(\bfq). b J 0 b ( q ) . Jlog 6 ( T t b ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\text{Jlog}_6(\bfT_{tb}) Jlog 6 ( T t b ) Jlog 6 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\text{Jlog}_6 Jlog 6 Jlog 6 ( T ) : = ∂ log 6 ( T ) ∂ T \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\text{Jlog}_6(\bfT) := \frac{\partial \log_6(\bfT)}{\partial \bfT} Jlog 6 ( T ) := ∂ T ∂ l o g 6 ( T ) Jlog6 (docs ) in Pinocchio.
Derivation of the pose task Jacobian
Let's derive the formula of our pose task Jacobian. Derivatives on manifolds is a bit verbose, so brace yourselves (and check out the micro Lie theory for support). We apply the chain rule carefully:
J : = ∂ e ∂ q = ∂ log 6 ( T b t ) ∂ q = ∂ log 6 ( T b 0 T 0 t ) ∂ q = ∂ log 6 ( T b 0 T 0 t ) ∂ T b 0 ∂ T b 0 ∂ T 0 b ∂ T 0 b ∂ q \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bfJ & := \frac{\partial \bfe}{\partial \bfq} \\
& = \frac{\partial \log_6(\bfT_{bt})}{\partial \bfq} \\
& = \frac{\partial \log_6(\bfT_{b0} \bfT_{0t})}{\partial \bfq} \\
& = \frac{\partial \log_6(\bfT_{b0} \bfT_{0t})}{\partial \bfT_{b0}} \frac{\partial \bfT_{b0}}{\partial \bfT_{0b}} \frac{\partial \bfT_{0b}}{\partial \bfq}
\end{align*} J := ∂ q ∂ e = ∂ q ∂ log 6 ( T b t ) = ∂ q ∂ log 6 ( T b 0 T 0 t ) = ∂ T b 0 ∂ log 6 ( T b 0 T 0 t ) ∂ T 0 b ∂ T b 0 ∂ q ∂ T 0 b In the last step, we have assume that T 0 t \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfT_{0t} T 0 t ∂ T 0 t \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\partial \bfT_{0t} ∂ T 0 t Jlog6 and the micro Lie theory writeup. The first one is about the derivative of the log of a product:
∂ log 6 ( A B ) ∂ A = ∂ log 6 ( A B ) ∂ ( A B ) ∂ ( A B ) ∂ A = Jlog 6 ( A B ) A d B − 1 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\frac{\partial \log_6(\bfA \bfB)}{\partial \bfA} = \frac{\partial \log_6(\bfA \bfB)}{\partial (\bfA \bfB)} \frac{\partial (\bfA \bfB)}{\partial \bfA} = \text{Jlog}_6(\bfA \bfB) \mathbf{Ad}_{\bfB}^{-1} ∂ A ∂ log 6 ( A B ) = ∂ ( A B ) ∂ log 6 ( A B ) ∂ A ∂ ( A B ) = Jlog 6 ( A B ) Ad B − 1 The second identity is about the derivative of the inverse of a transform (equation (62) in the micro Lie theory):
∂ M − 1 ∂ M = − A d M \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\frac{\partial \bfM^{-1}}{\partial \bfM} = -\mathbf{Ad}_{\bfM} ∂ M ∂ M − 1 = − Ad M In our context, applying these two formulas yields:
J = Jlog 6 ( T b t ) A d T 0 t − 1 ( − A d T 0 b ) ∂ T 0 b ∂ q = − Jlog 6 ( T b t ) A d T t b ∂ T 0 b ∂ q \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bfJ & = \text{Jlog}_6(\bfT_{bt}) \mathbf{Ad}^{-1}_{\bfT_{0t}} (-\mathbf{Ad}_{\bfT_{0b}}) \frac{\partial \bfT_{0b}}{\partial \bfq} \\
& = -\text{Jlog}_6(\bfT_{bt}) \mathbf{Ad}_{\bfT_{tb}} \frac{\partial \bfT_{0b}}{\partial \bfq}
\end{align*} J = Jlog 6 ( T b t ) Ad T 0 t − 1 ( − Ad T 0 b ) ∂ q ∂ T 0 b = − Jlog 6 ( T b t ) Ad T t b ∂ q ∂ T 0 b So far we have established that J ( q ) = − Jlog 6 ( T b t ) A d T t b b J 0 b ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ(\bfq) = -\text{Jlog}_6(\bfT_{bt}) \mathbf{Ad}_{\bfT_{tb}} {}_b \bfJ_{0b}(\bfq) J ( q ) = − Jlog 6 ( T b t ) Ad T t b b J 0 b ( q ) Jlog 6 ( T − 1 ) A d T = Jlog 6 ( T ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\text{Jlog}_6(\bfT^{-1}) \mathbf{Ad}_{\bfT} = \text{Jlog}_6(\bfT) Jlog 6 ( T − 1 ) Ad T = Jlog 6 ( T )
log 6 ( T − 1 ) = − log 6 ( T ) ⇔ exp ( − τ ) = exp ( τ ) − 1 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\log_6(\bfT^{-1}) = -\log_6(\bfT) \ \Leftrightarrow \ \exp(-\bftau) = \exp(\bftau)^{-1} log 6 ( T − 1 ) = − log 6 ( T ) ⇔ exp ( − τ ) = exp ( τ ) − 1 Things don't commute in Lie groups and one usually needs to "unlearn" some of the algebra from R \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathbb{R} R log 6 ( A B ) ≠ log 6 ( A ) + log 6 ( B ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\log_6(\bfA \bfB) \neq \log_6(\bfA) + \log_6(\bfB) log 6 ( A B ) = log 6 ( A ) + log 6 ( B ) log 6 ( A B ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\log_6(\bfA \bfB) log 6 ( A B )
log 6 ( T − 1 ) = − log 6 ( T ) ∂ log 6 ( T − 1 ) ∂ T = − ∂ log 6 ( T ) ∂ T − Jlog 6 ( T − 1 ) A d T = − Jlog 6 ( T ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\log_6(\bfT^{-1}) & = -\log_6(\bfT) \\
\frac{\partial \log_6(\bfT^{-1})}{\partial \bfT} & = -\frac{\partial \log_6(\bfT)}{\partial \bfT} \\
-\text{Jlog}_6(\bfT^{-1}) \mathbf{Ad}_{\bfT} & = -\text{Jlog}_6(\bfT)
\end{align*} log 6 ( T − 1 ) ∂ T ∂ log 6 ( T − 1 ) − Jlog 6 ( T − 1 ) Ad T = − log 6 ( T ) = − ∂ T ∂ log 6 ( T ) = − Jlog 6 ( T ) Wrapping up, we have shown that J ( q ) = − Jlog 6 ( T b t ) A d T t b b J 0 b ( q ) = − Jlog 6 ( T t b ) b J 0 b ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ(\bfq) = -\text{Jlog}_6(\bfT_{bt}) \mathbf{Ad}_{\bfT_{tb}} {}_b \bfJ_{0b}(\bfq) = -\text{Jlog}_6(\bfT_{tb}) {}_b \bfJ_{0b}(\bfq) J ( q ) = − Jlog 6 ( T b t ) Ad T t b b J 0 b ( q ) = − Jlog 6 ( T t b ) b J 0 b ( q )
Effect of the log-derivative
The effect of the log-derivative Jlog 6 ( T t b ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\text{Jlog}_6(\bfT_{tb}) Jlog 6 ( T t b ) q ˙ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\qd q ˙
Log-derivative with a single non-singular task
Suppose that the pose task has a non-singular Jacobian, and we have a single task in our inverse kinematics problem. Surprisingly, in that case a simplification occurs and the log-derivative has no effect on the resulting velocity:
J ( q ) non-singular ⇒ [ J ( q ) q ˙ = − α e ( q ) ⇔ b J 0 b ( q ) q ˙ = − α e ( q ) ] \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ(\bfq) \text{ non-singular } \Rightarrow \left[
\bfJ(\bfq) \qd = -\alpha \bfe(\bfq) \ \Leftrightarrow \ {}_b \bfJ_{0b}(\bfq) \qd = -\alpha \bfe(\bfq)
\right] J ( q ) non-singular ⇒ [ J ( q ) q ˙ = − α e ( q ) ⇔ b J 0 b ( q ) q ˙ = − α e ( q ) ] Note the square brackets in this formula: the two Jacobian matrices are not equal, which would have been ∀ v , J ( q ) v = b J 0 b ( q ) v \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\forall \bfv, \bfJ(\bfq) \bfv = {}_b \bfJ_{0b}(\bfq) \bfv ∀ v , J ( q ) v = b J 0 b ( q ) v q ˙ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\qd q ˙
Here is one way to prove this formula:
J ( q ) q ˙ = − α e ( q ) q ˙ = − α J ( q ) − 1 e ( q ) q ˙ = − α b J 0 b ( q ) − 1 Jlog 6 ( T t b ) − 1 e ( q ) q ˙ = − α b J 0 b ( q ) − 1 e ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bfJ(\bfq) \qd & = -\alpha \bfe(\bfq)\\
\qd & = -\alpha \bfJ(\bfq)^{-1} \bfe(\bfq) \\
\qd & = -\alpha {}_b \bfJ_{0b}(\bfq)^{-1} \text{Jlog}_6(\bfT_{tb})^{-1} \bfe(\bfq) \\
\qd & = -\alpha {}_b \bfJ_{0b}(\bfq)^{-1} \bfe(\bfq)
\end{align*} J ( q ) q ˙ q ˙ q ˙ q ˙ = − α e ( q ) = − α J ( q ) − 1 e ( q ) = − α b J 0 b ( q ) − 1 Jlog 6 ( T t b ) − 1 e ( q ) = − α b J 0 b ( q ) − 1 e ( q ) where the last step derives from the general identity Jlog 6 ( T − 1 ) − 1 log 6 ( T ) = log 6 ( T ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\text{Jlog}_6(\bfT^{-1})^{-1} \log_6(\bfT) = \log_6(\bfT) Jlog 6 ( T − 1 ) − 1 log 6 ( T ) = log 6 ( T ) Jlog 3 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\text{Jlog}_3 Jlog 3 S O ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
SO(3) SO ( 3 ) θ = log 3 ( R ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bftheta = \log_3(\bfR) θ = log 3 ( R )
Jlog 3 ( R − 1 ) − 1 log 3 ( R ) = [ I − 1 − cos θ θ 2 [ − θ ] × + θ − sin θ θ 3 [ − θ ] × 2 ] θ = θ − ( … ) [ θ ] × θ + ( … ) [ θ ] × 2 θ = θ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\text{Jlog}_3(\bfR^{-1})^{-1} \log_3(\bfR) & = \left[\bfI - \frac{1 - \cos \theta}{\theta^2} [-\bftheta]_\times + \frac{\theta - \sin \theta}{\theta^3} [-\bftheta]_\times^2\right] \bftheta \\
& = \bftheta - \left(\ldots\right) [\bftheta]_\times \bftheta + \left(\ldots\right) [\bftheta]_\times^2 \bftheta \\
& = \bftheta
\end{align*} Jlog 3 ( R − 1 ) − 1 log 3 ( R ) = [ I − θ 2 1 − cos θ [ − θ ] × + θ 3 θ − sin θ [ − θ ] × 2 ] θ = θ − ( … ) [ θ ] × θ + ( … ) [ θ ] × 2 θ = θ where we used the fact that v × v = 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfv \times \bfv = \bfzero v × v = 0 v \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfv v S E ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
SE(3) SE ( 3 ) Jlog 6 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\text{Jlog}_6 Jlog 6 Jlog6 documentation , is left to the reader 😉 We can also check it numerically:
>>> import pinocchio as pin
>>> import numpy as np
>>> T = pin . SE3 . Random ()
>>> pin . log6 ( T )
v = - 0.0952361 1.04225 - 0.718962
w = - 0.85911 - 2.44664 0.51629
>>> pin . Motion ( np . linalg . inv ( pin . Jlog6 ( T . inverse ())) @ pin . log6 ( T ))
v = - 0.0952361 1.04225 - 0.718962
w = - 0.85911 - 2.44664 0.51629
where we called np.linalg.inv for illustrative purposes. (In practice, it is better to np.linalg.solve(A, b) rather than np.linalg.inv(A) @ b. Don't invert that matrix .)
Log-derivative with multiple weighted tasks
A key question in inverse kinematics arises when we have multiple tasks that cannot be all fulfilled at the same time. As of writing this note, the two main answers to this question are weighted and lexicographic optimization. In weighted optimization, we associate a weight w > 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
w > 0 w > 0 Pink , an inverse kinematics library in Python based on Pinocchio.
Before v0.8.0, the pose task in Pink implemented the frame Jacobian b J 0 b ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}_b \bfJ_{0b}(\bfq) b J 0 b ( q ) omnidirectional wheeled robot . Here is the resulting behavior in Pink v0.7.0:
Upgrading to Pink v0.8.0, which added the missing log-derivative to the Jacobian formula, running the same code results in:
The corresponding code is available in the omnidirectional_wheeled_robot.py example from the project repository. The numerical instability before v0.8.0 is related to the fact that this example weighs position and orientation coordinates differently, and that the task is in competition with a damping task. If we suppose no constraint, the quadratic program solved by the IK can be written as:
v ∗ = arg min v 1 2 v T P v + q T v ⇔ P v ∗ = − q \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfv^* = \arg\min_{\bfv} \frac{1}{2} \bfv^T \bfP \bfv + \bfq^T \bfv \ \Leftrightarrow \ \bfP \bfv^* = - \bfq v ∗ = arg v min 2 1 v T P v + q T v ⇔ P v ∗ = − q With our pose task and a damping task, the matrix P \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfP P q \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfq q
J l : = − Jlog 6 ( T t b ) J b : = b J 0 b ( q ) P = J b T J l T W J l J b + λ I q = − J b T J l T W e \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bfJ_l & := -\text{Jlog}_6(\bfT_{tb}) \\
\bfJ_b & := {}_b \bfJ_{0b}(\bfq) \\
\bfP & = \bfJ_b^T \bfJ_l^T \bfW \bfJ_l \bfJ_b + \lambda \bfI \\
\bfq & = -\bfJ_b^T \bfJ_l^T \bfW \bfe
\end{align*} J l J b P q := − Jlog 6 ( T t b ) := b J 0 b ( q ) = J b T J l T W J l J b + λ I = − J b T J l T W e where W \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfW W docs ). If there were no damping task (λ = 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\lambda = 0 λ = 0 P v ∗ = − q \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfP \bfv^* = -\bfq P v ∗ = − q ( W J l J b ) − T \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
(\bfW \bfJ_l \bfJ_b)^{-T} ( W J l J b ) − T
P v ∗ = − q J l J b v ∗ = − e J b v ∗ = − J l − 1 e = − e v ∗ = − J b − 1 e \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bfP \bfv^* & = -\bfq \\
\bfJ_l \bfJ_b \bfv^* & = -\bfe \\
\bfJ_b \bfv^* & = -\bfJ_l^{-1} \bfe = -\bfe \\
\bfv^* & = -\bfJ_b^{-1} \bfe
\end{align*} P v ∗ J l J b v ∗ J b v ∗ v ∗ = − q = − e = − J l − 1 e = − e = − J b − 1 e where we used again the identity J l − 1 e = e \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ_l^{-1} \bfe = \bfe J l − 1 e = e J = J l J b \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ = \bfJ_l \bfJ_b J = J l J b J b \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ_{b} J b λ > 0 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\lambda > 0 λ > 0
v ∗ = − [ J b + λ J l − 1 W − 1 J l − T J b − T ] − 1 e \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfv^* = -\left[ J_b + \lambda \bfJ_l^{-1} \bfW^{-1} \bfJ_l^{-T} \bfJ_b^{-T}\right]^{-1} \bfe v ∗ = − [ J b + λ J l − 1 W − 1 J l − T J b − T ] − 1 e Because of the damping task, the log-derivative J l \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ_l J l J b \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ_b J b
v w r o n g = − [ J b + λ W − 1 J b − T ] − 1 e \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfv_{wrong} = -\left[ J_b + \lambda \bfW^{-1} \bfJ_b^{-T}\right]^{-1} \bfe v w ro n g = − [ J b + λ W − 1 J b − T ] − 1 e The latter is the velocity that was computed by Pink v0.7.0, the former is the velocity computed by Pink v0.8.0.
To go further
A number of implementations out there got the pose task Jacobian wrong, including the one I wrote during my PhD in pymanoid ! Other libraries do include the log-derivative properly in their code, for instance the optimal control library Crocoddyl (see ResidualModelFramePlacementTpl<Scalar>::calcDiff() at line 56 ) or the motion planner HPP (see JacobianVisitor::operator()<SE3> at line 129 ). This note was written while fixing and writing proper unit tests for the pose task in Pink , an inverse kinematics based on Pinocchio. The most helpful read in this process was the micro Lie theory writeup.
In this post, we used right-plus and right-minus operators along with local frame Jacobians, which is for instance the design choice made in Pink . We could also have used left-plus and left-minus operators along with frame Jacobians in the world frame, which is for instance the design choice made in Tasks . There is a numerical-stability argument to be made in favor of storing body (local frame) rather than spatial (world frame) vectors, as for instance the instantaneous spatial twist of a mobile robot becomes larger and larger as the robot moves away from the origin of the world frame.
For orientation tasks in S O ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
SO(3) SO ( 3 ) orientation task Jacobians with quaternions , then implement a pose task in R 3 × S O ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathbb{R}^3 \times SO(3) R 3 × SO ( 3 ) R 3 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathbb{R}^3 R 3 S O ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
SO(3) SO ( 3 ) S E ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
SE(3) SE ( 3 ) S E ( 3 ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
SE(3) SE ( 3 )
Discussion
Feel free to post a comment by e-mail using the form below. Your e-mail address will not be disclosed.