Contact modes

Physical contacts can be modeled as degrees of constraints that mobile robots maintain while moving. They stem from the non-penetrability condition: if $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} d_{ij}$ is the distance between the closest pair of points, one belonging to a body $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} i$ and the other to a body $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} j \neq i$ , then

\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} d_{ij} \geq 0.

When $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} d_{ij} > 0$ , there is no contact and the two bodies may move freely. But as soon as $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} d_{ij} = 0$ , contact appears and constraints the respective motions of the two bodies.

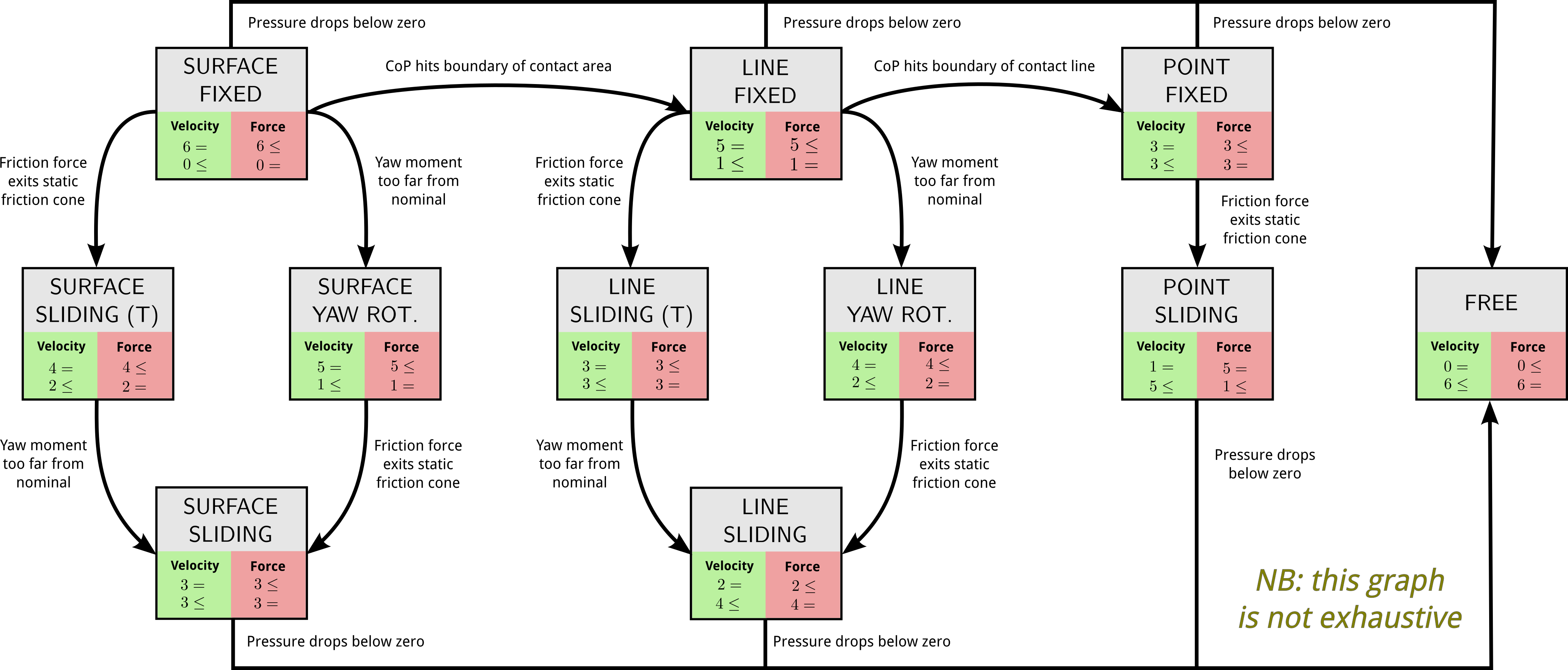
Definition from degrees of constraints¶

In rigid body dynamics, a body has six degrees of freedom, three for its translation and three for its orientation. Therefore, a contact can create between one and six degrees of constraints (DOC), depending on the number and arrangement of contact points between the contacting bodies.

Definition (Balkcom and Trinkle):: The mode of a contact is the set of degrees of constraints that it introduces between the two contacting bodies.

Common contact modes include:

Broken: When there is no contact (DOC: 0)
Sliding: When there is a relative translation between contact surfaces, accompanied or not by a rotation along the contact normal (DOC: 3 or 4)
Rolling: When one body in contact is rotating around a line on the other body, accompanied or not by a translation along that line (DOC: 2 or 3)
Fixed: When the contact is fully constrained (DOC: 6)

Complementarity in contact modes¶

Owing to the complementary relationship between motion and force vectors in screw theory, each degree of constraint on motions springs a degree of freedom on forces, and vice versa. For instance, a broken contact allows for free motions in the space $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} d_{ij} \geq 0$ delimited by the non-penetration condition, and fully constraints the contact wrench to $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} \boldsymbol{0}$ . Meanwhile, a fixed contact fully constraints motion vectors (velocities, accelerations, etc.) to $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} \boldsymbol{0}$ , and allows for free forces in the space $\def\bfA{\boldsymbol{A}} \def\bfB{\boldsymbol{B}} \def\bfC{\boldsymbol{C}} \def\bfD{\boldsymbol{D}} \def\bfE{\boldsymbol{E}} \def\bfF{\boldsymbol{F}} \def\bfG{\boldsymbol{G}} \def\bfH{\boldsymbol{H}} \def\bfI{\boldsymbol{I}} \def\bfJ{\boldsymbol{J}} \def\bfK{\boldsymbol{K}} \def\bfL{\boldsymbol{L}} \def\bfM{\boldsymbol{M}} \def\bfN{\boldsymbol{N}} \def\bfO{\boldsymbol{O}} \def\bfP{\boldsymbol{P}} \def\bfQ{\boldsymbol{Q}} \def\bfR{\boldsymbol{R}} \def\bfS{\boldsymbol{S}} \def\bfT{\boldsymbol{T}} \def\bfU{\boldsymbol{U}} \def\bfV{\boldsymbol{V}} \def\bfW{\boldsymbol{W}} \def\bfX{\boldsymbol{X}} \def\bfY{\boldsymbol{Y}} \def\bfZ{\boldsymbol{Z}} \def\bfalpha{\boldsymbol{\alpha}} \def\bfa{\boldsymbol{a}} \def\bfbeta{\boldsymbol{\beta}} \def\bfb{\boldsymbol{b}} \def\bfcd{\dot{\bfc}} \def\bfchi{\boldsymbol{\chi}} \def\bfc{\boldsymbol{c}} \def\bfd{\boldsymbol{d}} \def\bfe{\boldsymbol{e}} \def\bff{\boldsymbol{f}} \def\bfgamma{\boldsymbol{\gamma}} \def\bfg{\boldsymbol{g}} \def\bfh{\boldsymbol{h}} \def\bfi{\boldsymbol{i}} \def\bfj{\boldsymbol{j}} \def\bfk{\boldsymbol{k}} \def\bflambda{\boldsymbol{\lambda}} \def\bfl{\boldsymbol{l}} \def\bfm{\boldsymbol{m}} \def\bfn{\boldsymbol{n}} \def\bfomega{\boldsymbol{\omega}} \def\bfone{\boldsymbol{1}} \def\bfo{\boldsymbol{o}} \def\bfpdd{\ddot{\bfp}} \def\bfpd{\dot{\bfp}} \def\bfphi{\boldsymbol{\phi}} \def\bfp{\boldsymbol{p}} \def\bfq{\boldsymbol{q}} \def\bfr{\boldsymbol{r}} \def\bfsigma{\boldsymbol{\sigma}} \def\bfs{\boldsymbol{s}} \def\bftau{\boldsymbol{\tau}} \def\bftheta{\boldsymbol{\theta}} \def\bft{\boldsymbol{t}} \def\bfu{\boldsymbol{u}} \def\bfv{\boldsymbol{v}} \def\bfw{\boldsymbol{w}} \def\bfxi{\boldsymbol{\xi}} \def\bfx{\boldsymbol{x}} \def\bfy{\boldsymbol{y}} \def\bfzero{\boldsymbol{0}} \def\bfz{\boldsymbol{z}} \def\defeq{\stackrel{\mathrm{def}}{=}} \def\p{\boldsymbol{p}} \def\qdd{\ddot{\bfq}} \def\qd{\dot{\bfq}} \def\q{\boldsymbol{q}} \def\xd{\dot{x}} \def\yd{\dot{y}} \def\zd{\dot{z}} \bfF \bff \leq \boldsymbol{0}$ delimited by the friction model.

More generally, contact modes can be seen as the states of the discrete system of contact dynamics. Transitions between modes, known as contact switches, occur when certain guard conditions are crossed. For instance, when the contact force reaches the boundary of its friction cone, or when the center of pressure hits the boundary of the contact area. Here is an example of a subgraph with transitions between contact modes:

The complete automaton of the discrete system is symmetric and dense.

To go further¶

The article by Balkcom and Trinkle (2002) introduced several important ideas, including contact modes and the representation of contact conditions by polyhedral convex sets.

Discussion ¶

Feel free to post a comment by e-mail using the form below. Your e-mail address will not be disclosed.