The simplest object we can study in kinematics is the point , also known as
particle in classical mechanics. We can describe a point A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
A A B p A ∈ R 3 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^\mathcal{B} \bfp_A \in
\mathbb{R}^3 B p A ∈ R 3 coordinates in the reference frame B = ( B , B e x , B e y , B e z ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{B} = (B,
{}^\mathcal{B} \bfe_x, {}^\mathcal{B} \bfe_y, {}^\mathcal{B} \bfe_z) B = ( B , B e x , B e y , B e z )
Cartesian coordinates
The three vectors ( B e x , B e y , B e z ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
({}^\mathcal{B} \bfe_x, {}^\mathcal{B} \bfe_y,
{}^\mathcal{B} \bfe_z) ( B e x , B e y , B e z ) orthonormal basis of R 3 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathbb{R}^3 R 3 Cartesian coordinates of A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
A A
The signed distance x \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
x x
The signed distance y \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
y y
The signed distance z \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
z z
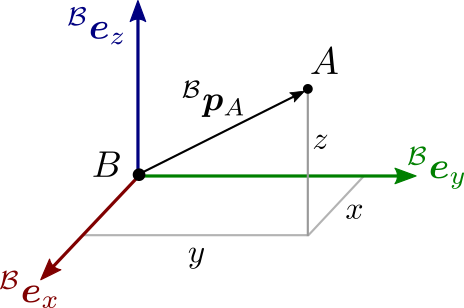
Mathematically:
B p A = [ x y z ] = x B e x + y B e y + z B e z \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^\mathcal{B} \bfp_A = \begin{bmatrix} x \\ y \\ z \end{bmatrix} = x\,{}^\mathcal{B} \bfe_x + y\,{}^\mathcal{B} \bfe_y + z\,{}^\mathcal{B} \bfe_z B p A = x y z = x B e x + y B e y + z B e z Graphically:
On a side note, the figure above introduces a color convention from computer
graphics where the x-axis (sagittal) is red, the y-axis (lateral) green and the
z-axis (vertical) blue. This convention was inherited from computer graphics
and is common in robotics software, for instance it is followed in RViz and OpenRAVE .
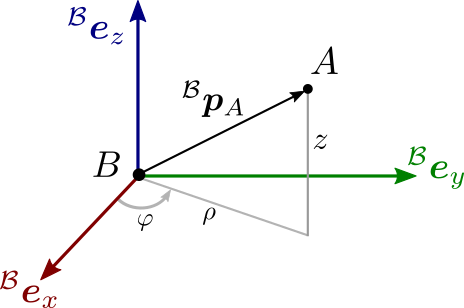
Cylindrical coordinates
Cylindrical coordinates represent the position of a point relative to an axis
of interest, typically the vertical z-axis, and a direction of interest,
typically the sagittal x-axis. They consist of three numbers:
The distance ρ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\rho ρ A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
A A
The angle φ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\varphi φ azimuthal angle (or just the azimuth , which sounds way cooler), between the vector from B \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
B B A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
A A e x \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfe_x e x
The axis coordinate z \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
z z
Mathematically, we can map the vector B χ A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^\mathcal{B}\bfchi_A B χ A
B χ A = [ ρ φ z ] ⟹ B p A ( B χ A ) = [ ρ cos φ ρ sin φ z ] \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^\mathcal{B} \bfchi_A = \begin{bmatrix} \rho \\ \varphi \\ z \end{bmatrix} \ \Longrightarrow
\ {}^\mathcal{B} \bfp_A({}^\mathcal{B} \bfchi_A) = \begin{bmatrix} \rho \cos \varphi \\ \rho \sin \varphi \\ z \end{bmatrix} B χ A = ρ φ z ⟹ B p A ( B χ A ) = ρ cos φ ρ sin φ z Graphically:
These coordinates are sometimes useful to analyze quantities that act on a body
frame of a car or mobile robot. For example, when an external disturbance is
applied to a humanoid robot ,
looking at the direction and amplitude of the disturbance in the horizontal
plane can be more insightful than looking at individual x- and y-coordinates.
Spherical coordinates
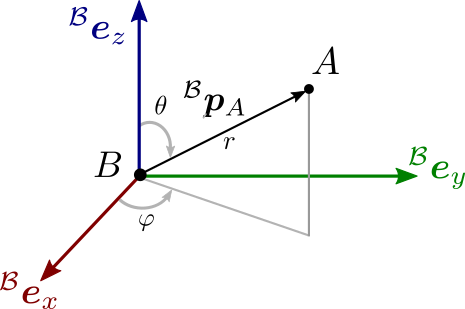
Spherical coordinates represent the position of a point by:
Its distance r \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
r r B \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
B B
The angle φ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\varphi φ
The angle θ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\theta θ polar , corresponding to the amount of rotation to apply in the resulting plane to go from the "pole" to the desired point.
Mathematically, we can map the vector B σ A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^\mathcal{B}\bfsigma_A B σ A
B σ A = [ r φ θ ] ⟹ B p A ( B σ A ) = [ r cos φ sin θ r sin φ sin θ r cos θ ] \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^\mathcal{B} \bfsigma_A = \begin{bmatrix} r \\ \varphi \\ \theta \end{bmatrix} \ \Longrightarrow
\ {}^\mathcal{B} \bfp_A({}^\mathcal{B} \bfsigma_A) = \begin{bmatrix} r \cos \varphi \sin \theta \\ r \sin \varphi \sin \theta \\ r \cos \theta \end{bmatrix} B σ A = r φ θ ⟹ B p A ( B σ A ) = r cos φ sin θ r sin φ sin θ r cos θ Graphically:
Observations
Difference between the object and its coordinates
These three coordinate systems can be used equivalently to represent the
position of our point A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
A A B \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{B} B A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
A A B p A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^\mathcal{B} \bfp_A B p A C p A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^\mathcal{C} p_A C p A C \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{C} C B \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\mathcal{B} B twists , etc.
Omitting the reference frame
When there is no ambiguity, the reference frame exponent is often dropped and
the position of point A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
A A p A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfp_A p A reference frame , so implicitly there is
always an underlying frame to any vector p A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfp_A p A
Discussion
Feel free to post a comment by e-mail using the form below. Your e-mail address will not be disclosed.