Wrench friction cones are 6D convex cones that characterize feasible contact wrenches, that is to say, wrenches a robot can apply while performing contact-stable motions. They generalize Coulomb friction cones to rigid bodies, and can also be used to encode other limitations such as joint torque limits.
Contact wrench cone¶
The net contact wrench cone (CWC) is the friction cone of the net contact wrench acting on a robot making multiple contacts, i.e. the sum of all contact wrenches. It can be represented as a set of feasible wrenches:
Since wrenches are screws, their coordinates are taken at a point with respect to a given frame. The same holds for the cone , here taken at the origin of and with respect to the inertial frame. Forces at each contact point are constrained to lie in the point's Coulomb friction cone . Friction cones can be either regular (with circular cross sections) or linearized (with polygonal cross sections).
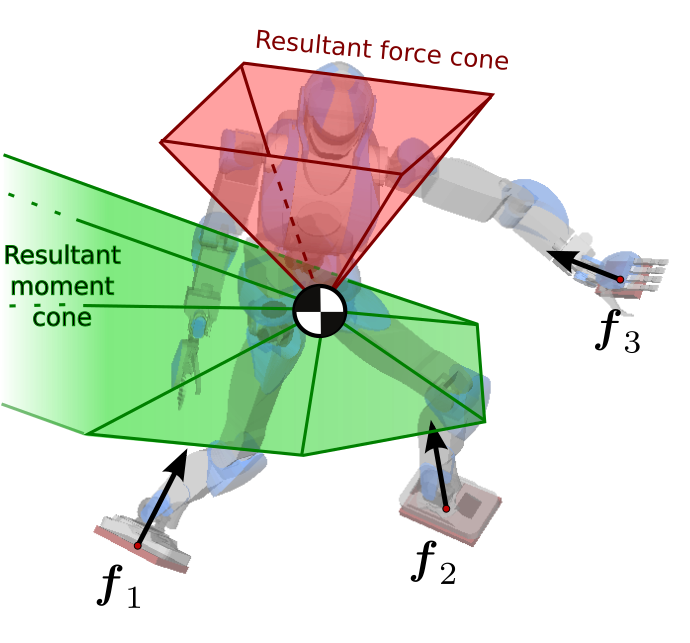
To the right is an artist view of the wrench cone for a humanoid robot making three point contacts. In this illustration we use linearized cones. The 6D wrench cone is represented by a red 3D force cone and a green 3D moment cone, yet keep in mind that it is only a drawing convenience. Force and moment are not independent, i.e. the 6D cone is not the direct product of these two 3D cones. If we fix the resultant force in the red cone, it will affect the shape of the green one, and conversely, if we fix the resultant moment (e.g. to zero, the linear inverted pendulum model discussed below), the red cone will change accordingly.
Wrench friction cone for surface contacts¶
In practice, the contacts that a humanoid makes are larger (to be precise: the wrench cone they provide is larger) than point contacts: they are surface contacts. The wrench cone of a surface contact can be represented by summing up Coulomb friction cones over all contact points on its contour (a proof of this property is e.g. recalled in Section III of this paper). In the case of a rectangular contact area, such as the foot or palm pad of a humanoid robot, and summing up linearized friction cones, the formula for these wrench cones can be written where:
Here denotes a feasible wrench expressed at the central frame of the rectangular contact area . Note how the matrix does not depend on the contact index , but only on the rectangle dimensions and friction coefficient .
Computing the contact wrench cone¶
Summing up over surface contacts, we can express the cone of feasible net wrenches in the same fashion as with point contacts:
Unlike with rectangular contact areas , we seldom have an analytical formula for the net cone because contact positions and orientations can be arbitrary over uneven terrains. A common solution is then to linearize friction cones and apply numerical polyhedral projection algorithms. The outcome of this calculation is again a linear inequality matrix :
This matrix now depends on contact positions and orientations, so it should be recomputed when contact locations change. It doesn't depend on the configuration of the robot though, so it can be used as long as the robot maintains the same set of contacts. If we only want to check if, at a given time, the robot can apply a given motion (centroidal momentum, i.e. center of mass acceleration and angular momentum), it is computationally more efficient to solve a quadratic program over feasible contact wrenches directly. But if we are optimizing a whole trajectory rather than a single time, computing the net wrench cone matrix and using it over the whole optimization can become more efficient.
Contact-stability areas and volumes¶
When additional constraints are imposed on the centroidal motion, the 6D net contact wrench cone reduces to lower-dimensional areas and volumes that can be used for planning or control.
Static-equilibrium polygon¶
When the robot is not moving, contact stability is characterized by the static equilibrium polygon: the configuration of the robot is feasible (sustainable) if and only if the center of mass lies in a specific polygon, which can be computed efficiently.
ZMP support area¶
When the robot moves in the linear inverted pendulum mode, that is, without too much torso gyration (to be precise: with conserved angular momentum, and keeping the center of mass in a plane), the CWC reduces to a ZMP support area.
Center of mass acceleration cone¶
When the robot moves without too much torso gyration (with a conserved angular momentum: ) but we want the center of mass to be allowed to go up and down, we can project the CWC to a 3D cone over center-of-mass accelerations that can be used e.g. for multi-contact locomotion.
To go further¶
Stability conditions are used extensively in motion generation, for instance in
multi-contact walking trajectory generation. Details on the
computation of the contact wrench cone by polyhedral projection can be found in
this paper. Sample
implementations of the algorithms can be found e.g. in the contact types
of pymanoid (Contact and ContactSet, in Python) or in
wrench-cone-lib (C++).
Wrench friction cones can represent all sorts of power limitations, including but not restricted to friction. One example is given by the torque-limited wrench cones used in this predictive controller for impact absorption, which can be projected into actuation-aware center-of-mass support areas.
Discussion ¶
You can subscribe to this Discussion's atom feed to stay tuned.
-

Manuel
Posted on
Thanks for the great summary of wrench cones in your article! I wanted to let you know that it could be nice to mention that the formulas presented here are regarding the linearized friction cone. Although it is nicely mentioned in the paper I feel like this could be valid information and would make the article even more helpful and self contained.
-

Stéphane
Posted on
Thank you for your feedback! Linearization was indeed implicit in the first paragraphs. It reads better now that it is explicit.
-
Feel free to post a comment by e-mail using the form below. Your e-mail address will not be disclosed.