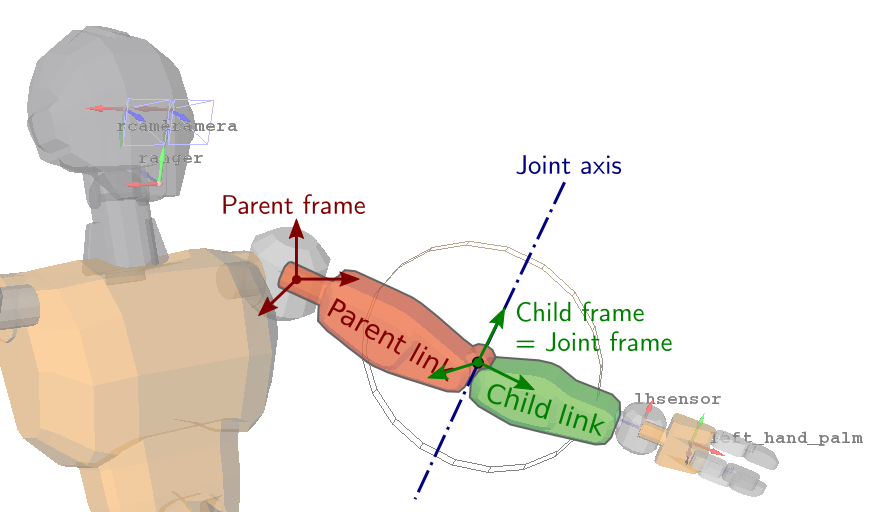
Kinematics of a revolute joint
Our robot model typically consists in a kinematic tree rooted at a special
link, the floating base or base link . Each link is a rigid body connected to one or more
others by joints that prevent motion
in some axes while allowing it on some others. Here is the example of a
revolute joint at the elbow of a humanoid robot:
In general there are six degrees of freedom between two rigid bodies,
corresponding to the three translation and three rotation coordinates of their
relative pose . A revolute joint allows
rotation around one axis only, the joint axis , thus leaving one degree of
freedom while applying five degrees of constraint between the two bodies. Such
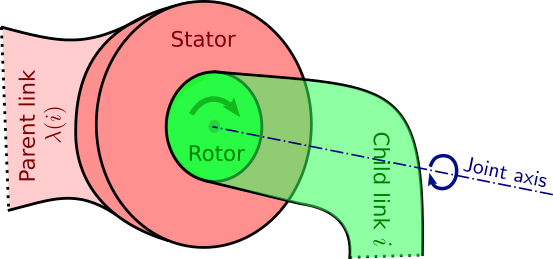
a joint is realized in practice by a rotary actuator, which looks like this:
Regardless of its design (brushless DC electric, series-elastic, quasi-direct
drive, …), the rotary actuator always has two main bodies when we look at it
from the outside: a stator and a rotor. The rotor rotates around (and is
typically symmetric around) the joint axis. The stator is attached to one link
and the rotor to the other, so that the actuator applies joint torque between
the two links. In the figure above we have attached the stator to the parent
link and the rotor to the child link, but it could very well have been the
other way round.
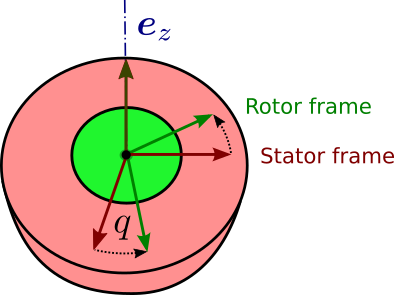
Relative pose of the child link
The Plücker transform X λ ( i ) , i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfX_{\lambda(i), i} X λ ( i ) , i i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
i i λ ( i ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\lambda(i) λ ( i )
X λ ( i ) , i = X λ ( i ) , s t a t o r ⋅ X s t a t o r , r o t o r ( q i ) ⋅ X r o t o r , i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfX_{\lambda(i), i} = \bfX_{\lambda(i), stator} \cdot \bfX_{stator, rotor}(q_i) \cdot \bfX_{rotor, i} X λ ( i ) , i = X λ ( i ) , s t a t or ⋅ X s t a t or , ro t or ( q i ) ⋅ X ro t or , i In the URDF convention, the child frame coincides with the joint frame ,
i.e. X r o t o r , i = I 6 × 6 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfX_{rotor, i} = \bfI_{6 \times 6} X ro t or , i = I 6 × 6 X λ ( i ) , s t a t o r \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfX_{\lambda(i), stator} X λ ( i ) , s t a t or X r o t o r , i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfX_{rotor, i} X ro t or , i q i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
q_i q i z \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
z z
The transform from the rotor frame to the stator frame is then:
X s t a t o r , r o t o r ( q i ) = [ cos ( q i ) − sin ( q i ) 0 0 0 0 sin ( q i ) cos ( q i ) 0 0 0 0 0 0 1 0 0 0 0 0 0 cos ( q i ) − sin ( q i ) 0 0 0 0 sin ( q i ) cos ( q i ) 0 0 0 0 0 0 1 ] \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfX_{stator, rotor}(q_i) =
\left[\begin{array} {ccc|ccc}
\cos(q_i) & -\sin(q_i) & 0 & 0 & 0 & 0 \\
\sin(q_i) & \cos(q_i) & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 \\
\hline
0 & 0 & 0 & \cos(q_i) & -\sin(q_i) & 0 \\
0 & 0 & 0 & \sin(q_i) & \cos(q_i) & 0 \\
0 & 0 & 0 & 0 & 0 & 1 \\
\end{array}
\right] X s t a t or , ro t or ( q i ) = cos ( q i ) sin ( q i ) 0 0 0 0 − sin ( q i ) cos ( q i ) 0 0 0 0 0 0 1 0 0 0 0 0 0 cos ( q i ) sin ( q i ) 0 0 0 0 − sin ( q i ) cos ( q i ) 0 0 0 0 0 0 1 That is, a pure rotation of angle q i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
q_i q i z \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
z z e i ≠ e z \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfe_i \neq \bfe_z e i = e z from their axis-angle representation
;-) In that case, the transform becomes:
X s t a t o r , r o t o r ( q i ) = [ R e i ( q i ) 0 3 × 3 0 3 × 3 R e i ( q i ) ] \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfX_{stator, rotor}(q_i) =
\left[\begin{array} {c|c}
\bfR_{\bfe_i}(q_i) & \bfzero_{3 \times 3} \\
\hline
\bfzero_{3 \times 3} & \bfR_{\bfe_i}(q_i)
\end{array}
\right] X s t a t or , ro t or ( q i ) = [ R e i ( q i ) 0 3 × 3 0 3 × 3 R e i ( q i ) ] Note that we didn't specify the frame of the Euclidean vector e i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfe_i e i s t a t o r e i = r o t o r e i = e i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^{stator} \bfe_i = {}^{rotor} \bfe_i = \bfe_i s t a t or e i = ro t or e i = e i
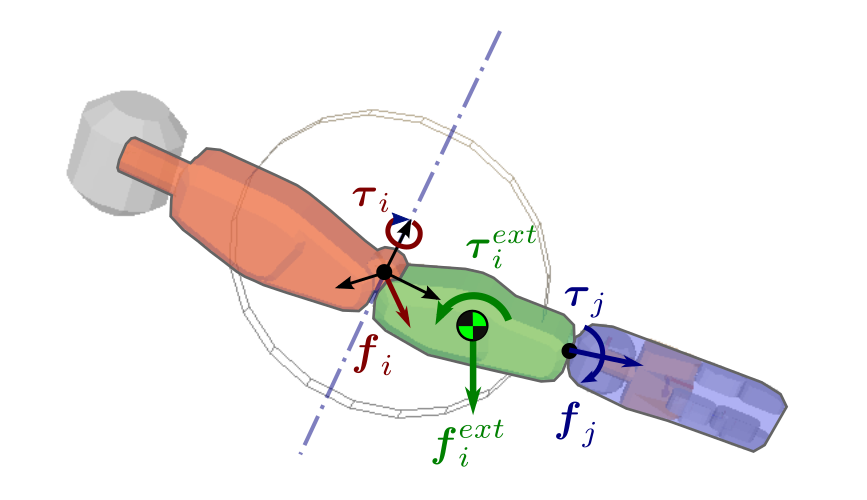
Velocity and velocity Jacobian of the link
The time derivative of the axis-angle rotation is R ˙ e ( q ) = q ˙ e × R e ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\dot{\bfR}_{\bfe}(q) =
\dot{q} \bfe \times \bfR_{\bfe}(q) R ˙ e ( q ) = q ˙ e × R e ( q )
R ˙ s t a t o r , r o t o r = q i ˙ e i × R s t a t o r , r o t o r X ˙ s t a t o r , r o t o r = q i ˙ [ e i 0 3 ] × X s t a t o r , r o t o r = q i ˙ s t a t o r s i × X s t a t o r , r o t o r \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\dot{\bfR}_{stator, rotor} & = \dot{q_i} \bfe_i \times \bfR_{stator, rotor} \\
\dot{\bfX}_{stator, rotor} & = \dot{q_i} \begin{bmatrix} \bfe_i \\ \bfzero_{3} \end{bmatrix} \times \bfX_{stator, rotor} = \dot{q_i} {}^{stator} \bfs_i \times \bfX_{stator, rotor}
\end{align*} R ˙ s t a t or , ro t or X ˙ s t a t or , ro t or = q i ˙ e i × R s t a t or , ro t or = q i ˙ [ e i 0 3 ] × X s t a t or , ro t or = q i ˙ s t a t or s i × X s t a t or , ro t or where we defined the motion vector s t a t o r s i : = [ e i 0 3 ] \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^{stator} \bfs_i :=
[\bfe_i\,\bfzero_{3}] s t a t or s i := [ e i 0 3 ] derivate the
transform X λ ( i ) , i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfX_{\lambda(i), i} X λ ( i ) , i
X ˙ λ ( i ) , i = λ ( i ) ( v i − v λ ( i ) ) × X λ ( i ) , i = X λ ( i ) , s t a t o r ⋅ X ˙ s t a t o r , r o t o r ⋅ X r o t o r , i = q ˙ i X λ ( i ) , s t a t o r ( s t a t o r s i × ) X s t a t o r , r o t o r X r o t o r , i = q ˙ i λ ( i ) s i × X λ ( i ) , s t a t o r X s t a t o r , r o t o r X r o t o r , i = q ˙ i λ ( i ) s i × X λ ( i ) , i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\dot{\bfX}_{\lambda(i), i} = {}^{\lambda(i)} (\bfv_i - \bfv_{\lambda(i)}) \times \bfX_{\lambda(i), i} & = \bfX_{\lambda(i), stator} \cdot \dot{\bfX}_{stator, rotor} \cdot \bfX_{rotor, i} \\
& = \dot{q}_i \bfX_{\lambda(i), stator} ({}^{stator} \bfs_i \times) \bfX_{stator, rotor} \bfX_{rotor, i} \\
& = \dot{q}_i {}^{\lambda(i)} \bfs_i \times \bfX_{\lambda(i), stator} \bfX_{stator, rotor} \bfX_{rotor, i} \\
& = \dot{q}_i {}^{\lambda(i)} \bfs_i \times \bfX_{\lambda(i), i}
\end{align*} X ˙ λ ( i ) , i = λ ( i ) ( v i − v λ ( i ) ) × X λ ( i ) , i = X λ ( i ) , s t a t or ⋅ X ˙ s t a t or , ro t or ⋅ X ro t or , i = q ˙ i X λ ( i ) , s t a t or ( s t a t or s i × ) X s t a t or , ro t or X ro t or , i = q ˙ i λ ( i ) s i × X λ ( i ) , s t a t or X s t a t or , ro t or X ro t or , i = q ˙ i λ ( i ) s i × X λ ( i ) , i This implies that λ ( i ) ( v i − v λ ( i ) ) = q ˙ i λ ( i ) s i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
{}^{\lambda(i)} (\bfv_i - \bfv_{\lambda(i)}) =
\dot{q}_i {}^{\lambda(i)} \bfs_i λ ( i ) ( v i − v λ ( i ) ) = q ˙ i λ ( i ) s i
v i = v λ ( i ) + s i ( q ) q ˙ i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfv_i = \bfv_{\lambda(i)} + \bfs_i(\bfq) \dot{q}_i v i = v λ ( i ) + s i ( q ) q ˙ i where s i ( q ) = X w o r l d , λ ( i ) ( q ) λ ( i ) s i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfs_i(\bfq) = \bfX_{world, \lambda(i)}(\bfq)
{}^{\lambda(i)} \bfs_i s i ( q ) = X w or l d , λ ( i ) ( q ) λ ( i ) s i q ˙ i ∈ R \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\dot{q}_i \in
\mathbb{R} q ˙ i ∈ R v i ∈ M 6 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfv_i \in \textsf{M}^6 v i ∈ M 6 s i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfs_i s i j \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
j j n j \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
n_j n j q j ∈ R n j \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfq_j \in \mathbb{R}^{n_j} q j ∈ R n j 6 × n j \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
6 \times
n_j 6 × n j S ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfS(\bfq) S ( q ) v i = v λ ( i ) + S ( q ) q ˙ j \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfv_i =
\bfv_{\lambda(i)} + \bfS(\bfq) \dot{\bfq}_j v i = v λ ( i ) + S ( q ) q ˙ j
v i = s i ( q ) q ˙ i + s λ ( i ) ( q ) q ˙ λ ( i ) + ⋯ + S b a s e ( q ) q ˙ b a s e = J i ( q ) q ˙ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfv_i
= \bfs_i(\bfq) \dot{q}_i + \bfs_{\lambda(i)}(\bfq) \dot{q}_{\lambda(i)} + \cdots + \bfS_{base}(\bfq) \dot{\bfq}_{base}
= \bfJ_i(\bfq) \dot{\bfq} v i = s i ( q ) q ˙ i + s λ ( i ) ( q ) q ˙ λ ( i ) + ⋯ + S ba se ( q ) q ˙ ba se = J i ( q ) q ˙ where J i ( q ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfJ_i(\bfq) J i ( q ) 6 × n \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
6 \times n 6 × n i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
i i [ q b a s e , … , q i , … ] \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
[\bfq_{base}, \ldots, q_i,
\ldots] [ q ba se , … , q i , … ] q \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfq q inverse kinematics is the
matrix thus derived.
Dynamics of a revolute joint
While kinematics derives from the composition of transforms X C A = X C B X B A \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfX_{CA} =
\bfX_{CB} \bfX_{BA} X C A = X CB X B A
I i a i + v i × ∗ I i v i = w i n e t \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfI_i \bfa_i + \bfv_i \times^* \bfI_i \bfv_i = \bfw^{net}_i I i a i + v i × ∗ I i v i = w i n e t where a i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfa_i a i I i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfI_i I i w i n e t \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw^{net}_i w i n e t τ i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\tau_i τ i
Forces acting on the link
By convention, we write w i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw_{i} w i parent link λ ( i ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\lambda(i) λ ( i ) i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
i i
w i n e t = w i + w i e x t − ∑ j ∈ s o n s ( i ) w j \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw^{net}_i = \bfw_i + \bfw_i^\mathit{ext} - \sum_{j \in \mathrm{sons}(i)} \bfw_j w i n e t = w i + w i ext − j ∈ sons ( i ) ∑ w j where w i e x t \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw^{ext}_i w i e x t
The force w i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw_i w i
Joint forces: w i j o i n t = ( s i ⋅ w i ) s i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw_i^{joint} = (\bfs_i \cdot \bfw_i) \bfs_i w i j o in t = ( s i ⋅ w i ) s i ∥ s i ∥ = 1 \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\| \bfs_i \| = 1 ∥ s i ∥ = 1 ( s i ⋅ w i ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
(\bfs_i \cdot \bfw_i) ( s i ⋅ w i )
s i ⋅ w i = ( X w o r l d , i i s i ) ⋅ ( X w o r l d , i ∗ i w i ) = i s i ⊤ X w o r l d , i ⊤ X w o r l d , i ∗ i w i = i s i ⋅ i w i = e i ⋅ i τ i = τ i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\begin{align*}
\bfs_i \cdot \bfw_i
& = (\bfX_{world, i} {}^i \bfs_i) \cdot (\bfX_{world, i}^* {}^i \bfw_i) \\
& = {}^i \bfs_i^\top \bfX_{world, i}^\top \bfX_{world, i}^* {}^i \bfw_i \\
& = {}^i \bfs_i \cdot {}^i \bfw_i \\
& = \bfe_i \cdot {}^i \bftau_i \\
& = \tau_i
\end{align*} s i ⋅ w i = ( X w or l d , i i s i ) ⋅ ( X w or l d , i ∗ i w i ) = i s i ⊤ X w or l d , i ⊤ X w or l d , i ∗ i w i = i s i ⋅ i w i = e i ⋅ i τ i = τ i
Internal forces: w i i n t = i s i × i w i × i s i = w i − ( i s i ⋅ i w i ) i s i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw_i^{int} = {}^i \bfs_i \times {}^i \bfw_i \times {}^i \bfs_i
= \bfw_i - ({}^i \bfs_i \cdot {}^i \bfw_i) {}^i \bfs_i w i in t = i s i × i w i × i s i = w i − ( i s i ⋅ i w i ) i s i a.k.a. "everything
else". These are the linear forces and torques transmitted through the
mounting of the joint (screws, contacts between parts, any device that
implements a degree of constraint). They don't affect the robot's motion, but
they may be relevant to other robotic activities such as "making sure things
don't break".
This shows how, if our rotary actuator is able to control the torque
τ i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\tau_i τ i i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
i i w i j o i n t = τ i s i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw_i^{joint} = \tau_i \bfs_i w i j o in t = τ i s i τ i = S i ⊤ w i j o i n t = S i ⊤ w i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bftau_i = \bfS_i^\top \bfw^{joint}_i = \bfS_i^\top \bfw_i τ i = S i ⊤ w i j o in t = S i ⊤ w i S i ⊤ \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfS_i^\top S i ⊤
Note that, from the usual convention that w i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\bfw_i w i τ i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\tau_i τ i to our link i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
i i − τ i \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
-\tau_i − τ i λ ( i ) \def\bfA{\boldsymbol{A}}
\def\bfB{\boldsymbol{B}}
\def\bfC{\boldsymbol{C}}
\def\bfD{\boldsymbol{D}}
\def\bfE{\boldsymbol{E}}
\def\bfF{\boldsymbol{F}}
\def\bfG{\boldsymbol{G}}
\def\bfH{\boldsymbol{H}}
\def\bfI{\boldsymbol{I}}
\def\bfJ{\boldsymbol{J}}
\def\bfK{\boldsymbol{K}}
\def\bfL{\boldsymbol{L}}
\def\bfM{\boldsymbol{M}}
\def\bfN{\boldsymbol{N}}
\def\bfO{\boldsymbol{O}}
\def\bfP{\boldsymbol{P}}
\def\bfQ{\boldsymbol{Q}}
\def\bfR{\boldsymbol{R}}
\def\bfS{\boldsymbol{S}}
\def\bfT{\boldsymbol{T}}
\def\bfU{\boldsymbol{U}}
\def\bfV{\boldsymbol{V}}
\def\bfW{\boldsymbol{W}}
\def\bfX{\boldsymbol{X}}
\def\bfY{\boldsymbol{Y}}
\def\bfZ{\boldsymbol{Z}}
\def\bfalpha{\boldsymbol{\alpha}}
\def\bfa{\boldsymbol{a}}
\def\bfbeta{\boldsymbol{\beta}}
\def\bfb{\boldsymbol{b}}
\def\bfcd{\dot{\bfc}}
\def\bfchi{\boldsymbol{\chi}}
\def\bfc{\boldsymbol{c}}
\def\bfd{\boldsymbol{d}}
\def\bfe{\boldsymbol{e}}
\def\bff{\boldsymbol{f}}
\def\bfgamma{\boldsymbol{\gamma}}
\def\bfg{\boldsymbol{g}}
\def\bfh{\boldsymbol{h}}
\def\bfi{\boldsymbol{i}}
\def\bfj{\boldsymbol{j}}
\def\bfk{\boldsymbol{k}}
\def\bflambda{\boldsymbol{\lambda}}
\def\bfl{\boldsymbol{l}}
\def\bfm{\boldsymbol{m}}
\def\bfn{\boldsymbol{n}}
\def\bfomega{\boldsymbol{\omega}}
\def\bfone{\boldsymbol{1}}
\def\bfo{\boldsymbol{o}}
\def\bfpdd{\ddot{\bfp}}
\def\bfpd{\dot{\bfp}}
\def\bfphi{\boldsymbol{\phi}}
\def\bfp{\boldsymbol{p}}
\def\bfq{\boldsymbol{q}}
\def\bfr{\boldsymbol{r}}
\def\bfsigma{\boldsymbol{\sigma}}
\def\bfs{\boldsymbol{s}}
\def\bftau{\boldsymbol{\tau}}
\def\bftheta{\boldsymbol{\theta}}
\def\bft{\boldsymbol{t}}
\def\bfu{\boldsymbol{u}}
\def\bfv{\boldsymbol{v}}
\def\bfw{\boldsymbol{w}}
\def\bfxi{\boldsymbol{\xi}}
\def\bfx{\boldsymbol{x}}
\def\bfy{\boldsymbol{y}}
\def\bfzero{\boldsymbol{0}}
\def\bfz{\boldsymbol{z}}
\def\defeq{\stackrel{\mathrm{def}}{=}}
\def\p{\boldsymbol{p}}
\def\qdd{\ddot{\bfq}}
\def\qd{\dot{\bfq}}
\def\q{\boldsymbol{q}}
\def\xd{\dot{x}}
\def\yd{\dot{y}}
\def\zd{\dot{z}}
\lambda(i) λ ( i )