ZMP support areas for
multi-contact locomotion

Stéphane Caron
LIRMM, CNRS-UM2
Work with Q.-C. Pham & Y. Nakamura
Journées Nationales de la Robotique Humanoïde
June 23, 2016

Walking on flat floors

• Start from a footstep plan

Walking on flat floors

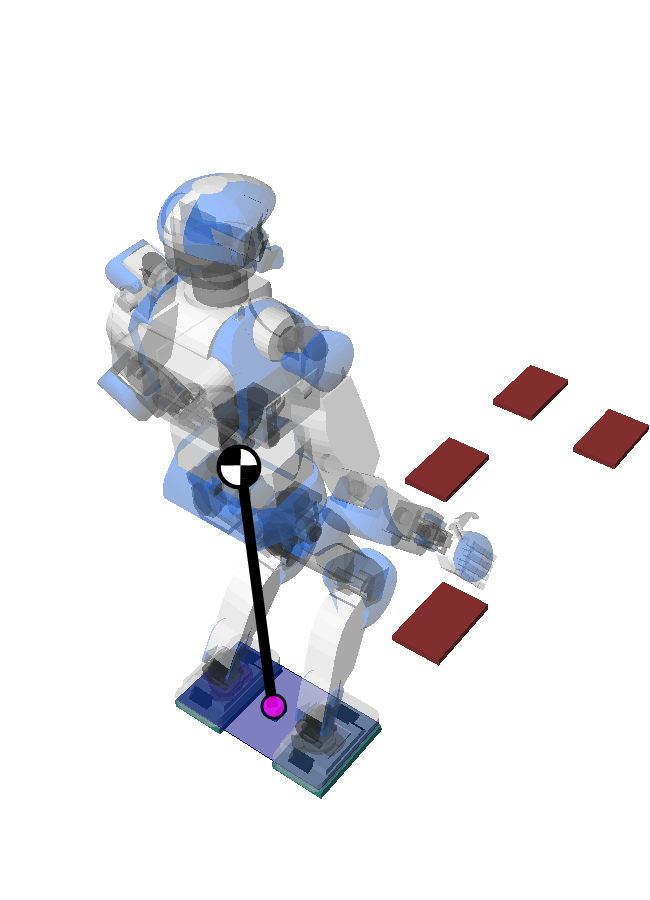
• Start from a footstep plan
• Regulate system dynamics around the Linear Inverted Pendulum Mode (LIPM)

Walking on flat floors

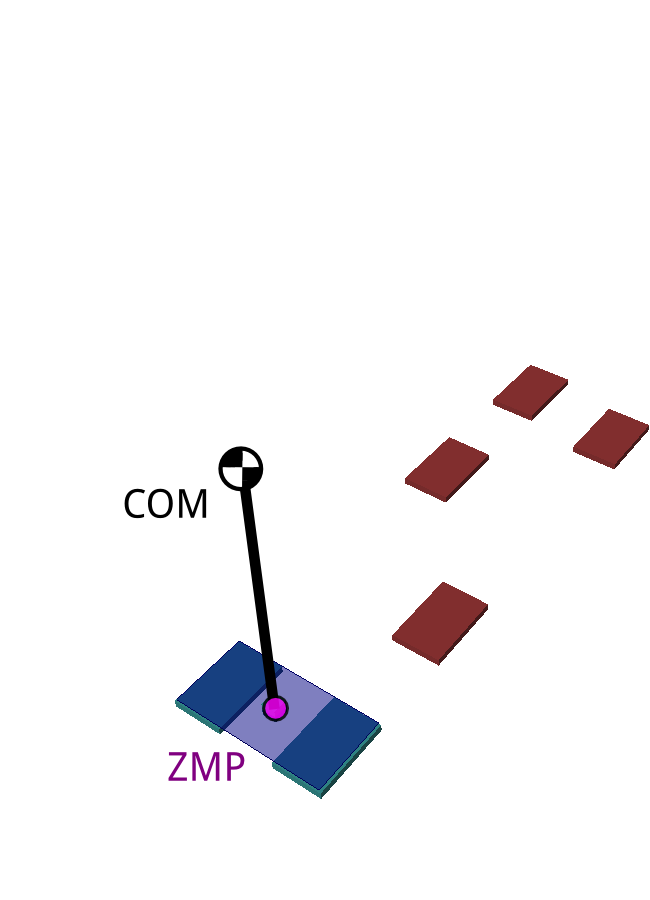
• Start from a footstep plan
• Regulate system dynamics around the Linear Inverted Pendulum Mode (LIPM)
• LIPM has simplified:
  • Dynamics:  ${\ddot{x}}_G={\omega }^2(x_G-x_Z)$
  • Contact stability criterion:
    ZMP inside the support polygon

Walking on flat floors

• Start from a footstep plan
• Regulate system dynamics around the Linear Inverted Pendulum Mode (LIPM)
• LIPM has simplified:
  • Dynamics:  ${\ddot{x}}_G={\omega }^2(x_G-x_Z)$
  • Contact stability criterion:
    ZMP inside the support polygon
• Plan a trajectory for the pendulum

Walking on flat floors

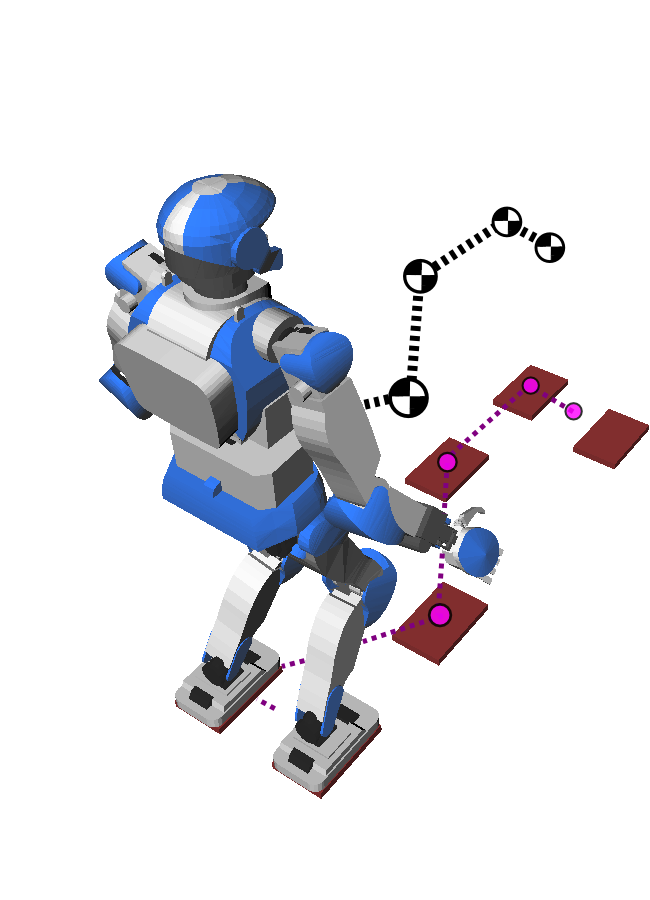
• Start from a footstep plan
• Regulate system dynamics around the Linear Inverted Pendulum Mode (LIPM)
• LIPM has simplified:
  • Dynamics:  ${\ddot{x}}_G={\omega }^2(x_G-x_Z)$
  • Contact stability criterion:
    ZMP inside the support polygon
• Plan a trajectory for the pendulum
• Send it as reference to a whole-body controller

Question

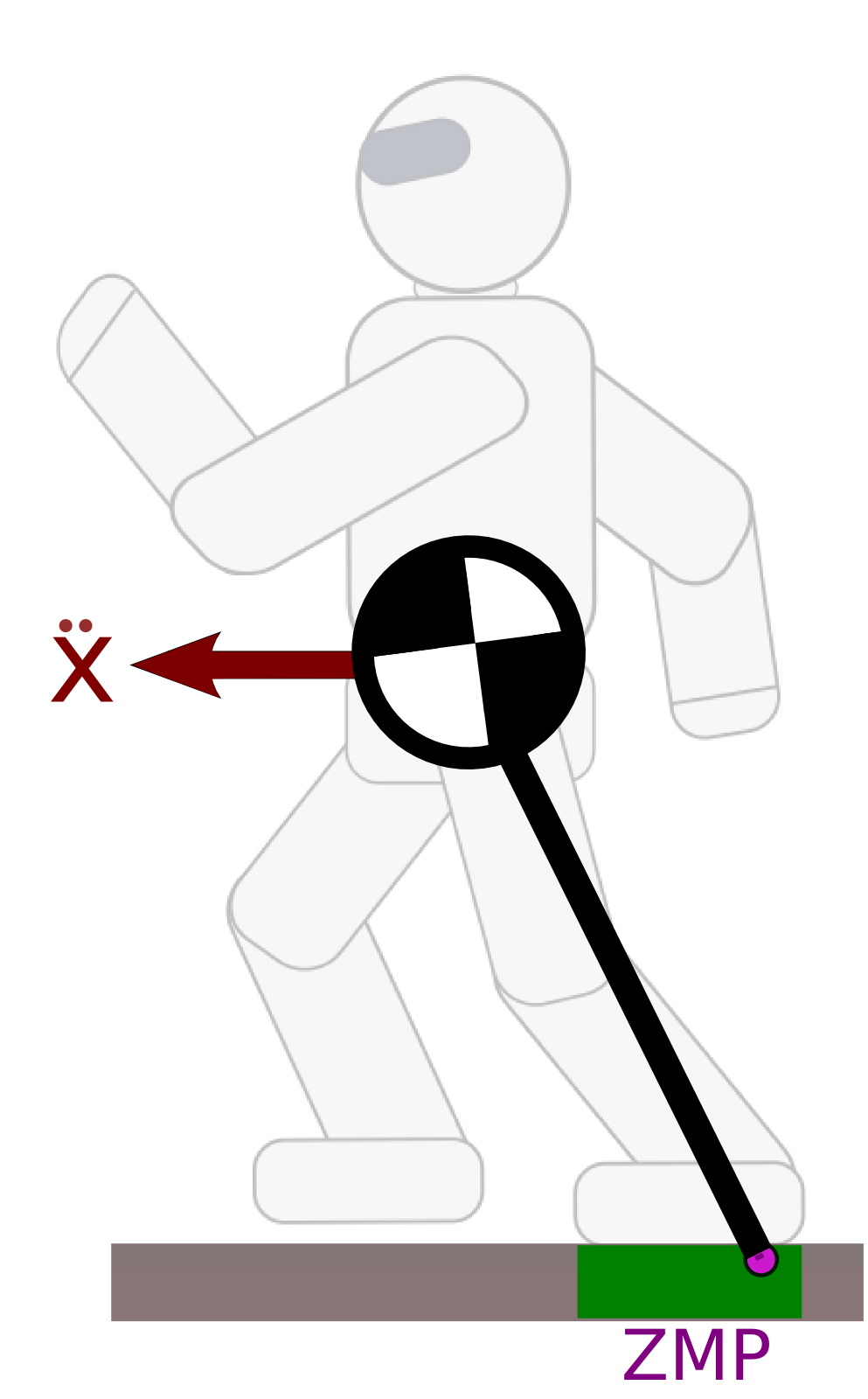
Zero-tilting Moment Point

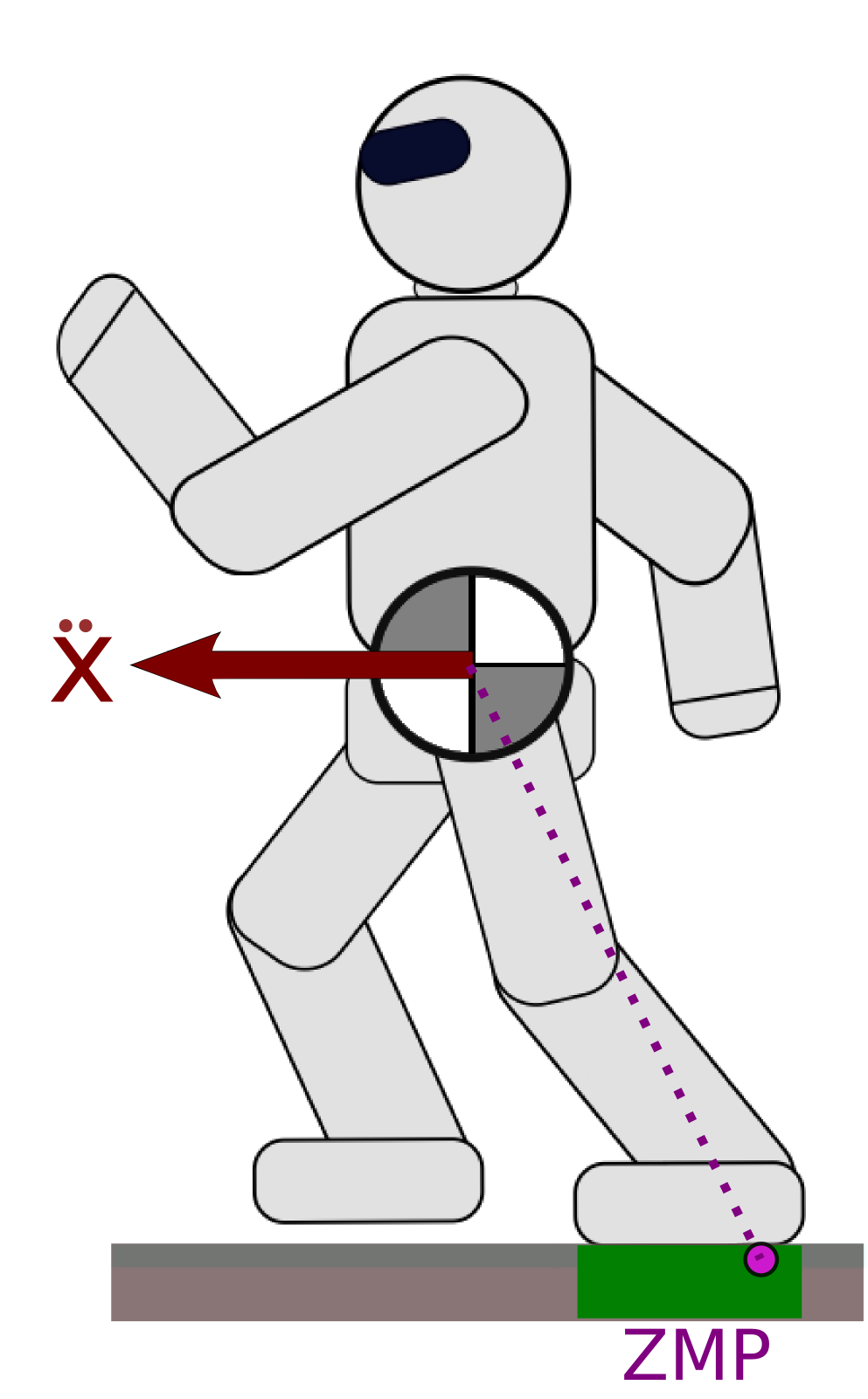
Definition

The ZMP is traditionally defined as the point on the floor where the moment of the contact wrench is parallel to the surface normal (Sardain & Bessonnet, 2004).

Intuition

The point at which the robot “applies its weight”.

Contact stability

The ZMP must lie inside the support polygon (convex hull of ground contact points).¹

Limitations

• This definition requires a single “floor” surface (no multi-contact)
• The support polygon does not account for frictional limits (slippage, yaw rotations).

Contact stability

What wrenches are feasible under frictional contacts?

Weak Contact Stability

A motion or wrench is weak contact stable iff it can be realized by contact forces inside their friction cones.

Contact Wrench Cone

Friction cones can be combined as Contact Wrench Cone (CWC) at the COM—see e.g. (Caron et al., 2015).
By construction,

ZMP of a Wrench

The ZMP is mathematically defined from a wrench (Sardain & Bessonnet, 2004). The ZMP in the plane $\Pi (O,n)$ of normal $n$ containing $O$ is the point such that $n\times {\tau }_Z=0$, that is:

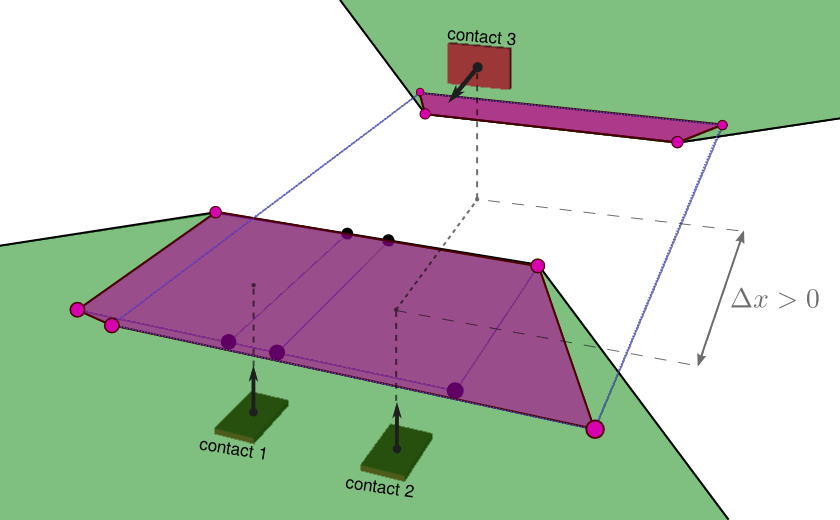
We define the full support area $S$ as the image of the CWC by this equation.

Contribution 1

Good news! This area can be computed geometrically:

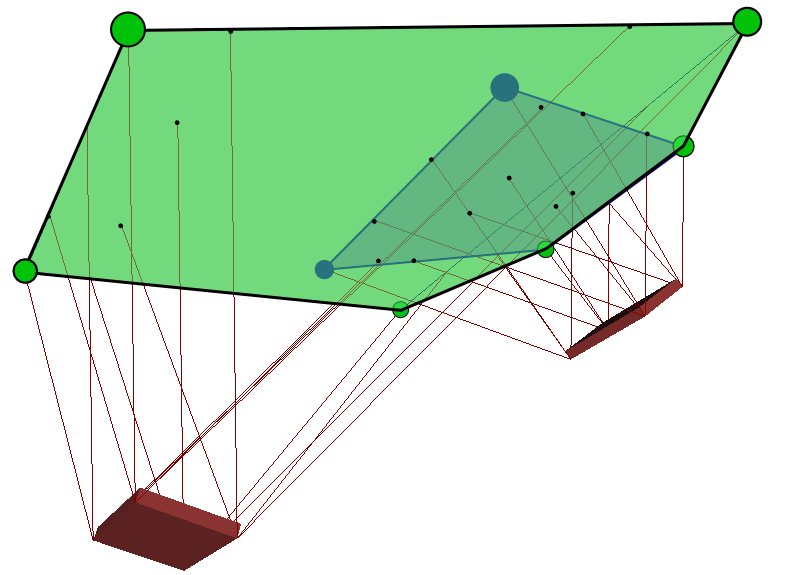
Contribution 1

Bad news! It is not always a polygon:

Centroidal dynamics

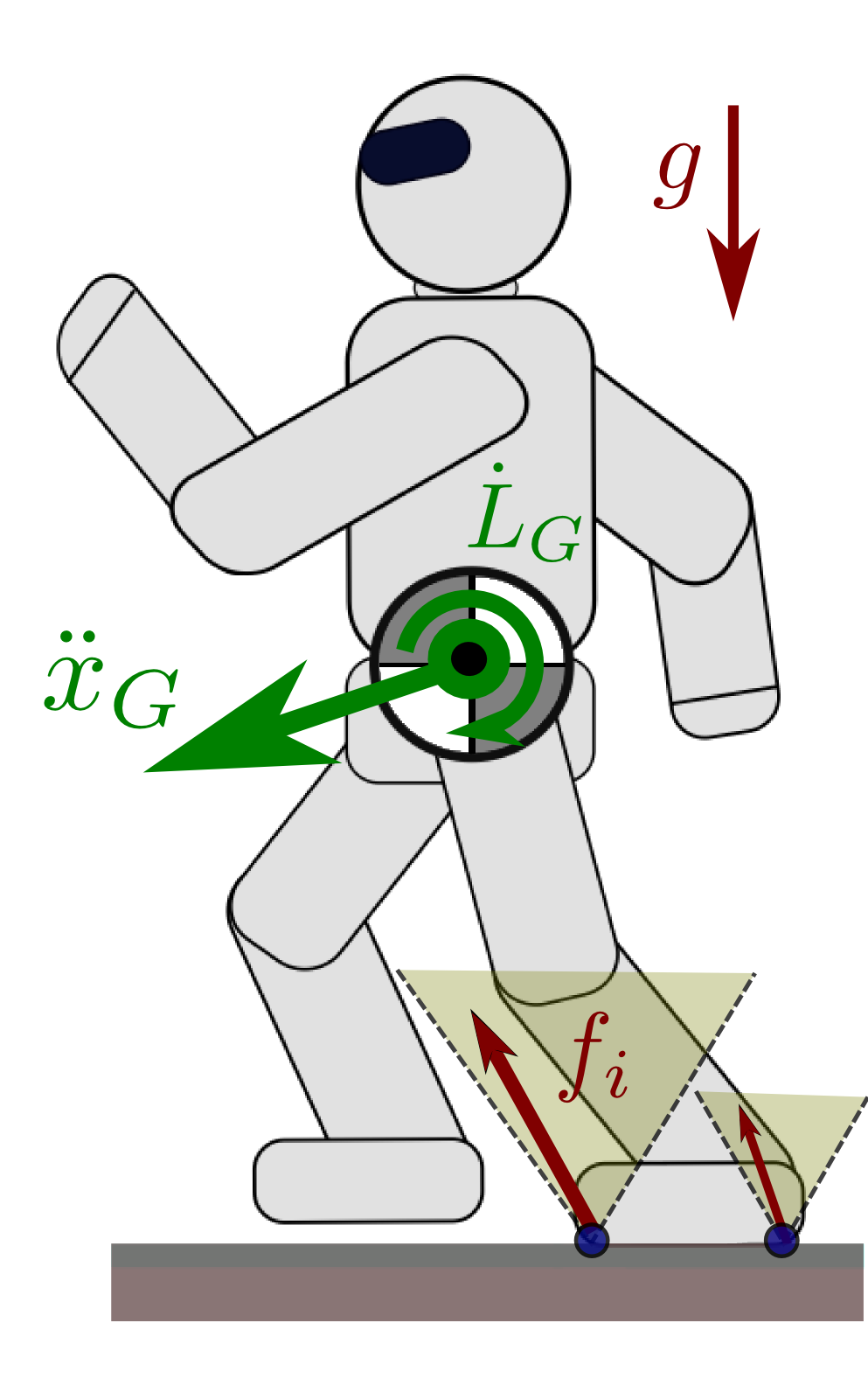
The Newton-Euler equations of the system are:

• $m$ and $g$: total mass and gravity vector
• ${\ddot{x}}_G$: acceleration of the center of mass (COM)
• ${\dot{L}}_G$: rate of change of the angular momentum
• $f_i$: contact force received at contact point $C_i$

They show how the motion of unactuated DOFs results from interactions with the environment.

Linear Pendulum Mode

The Newton equation can be written equivalently:

where $x$ now denotes X-Y plane coordinates. The Linear Inverted Pendulum Mode (Kajita et al., 2001) is obtained by constraining:

The system dynamics become ${\ddot{x}}_G=\frac{g}{h}(x_Z-x_G)$.

Observation

The support area in the LIPM is smaller than the convex hull of contact points:

Contribution 2

We provide an algorithm to compute the support area corresponding to the system:

We call it the pendular support area.

Pendular Support Area

Pendular Support Area

Pendular Support Area

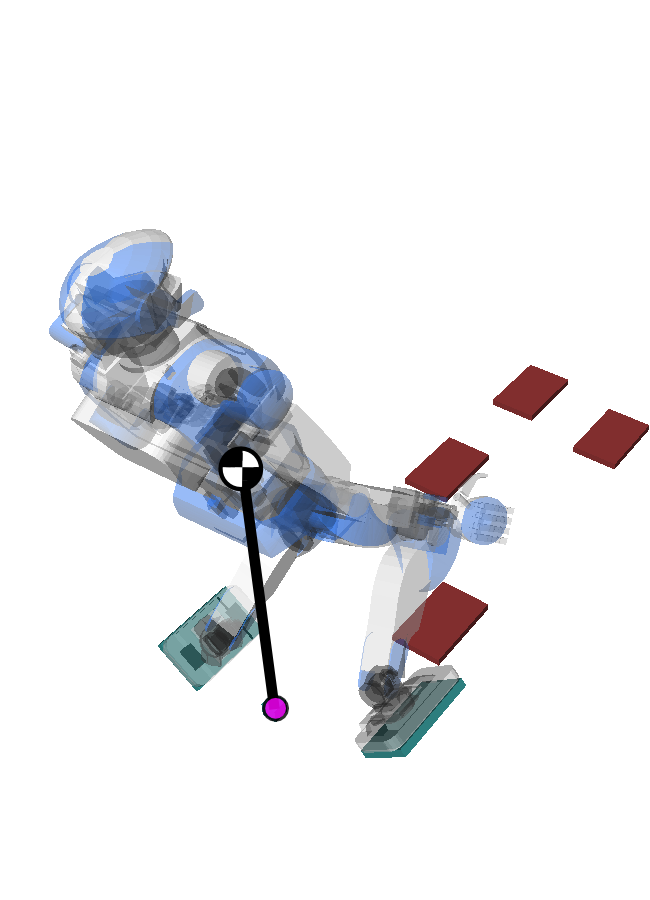
Pendular Support Area

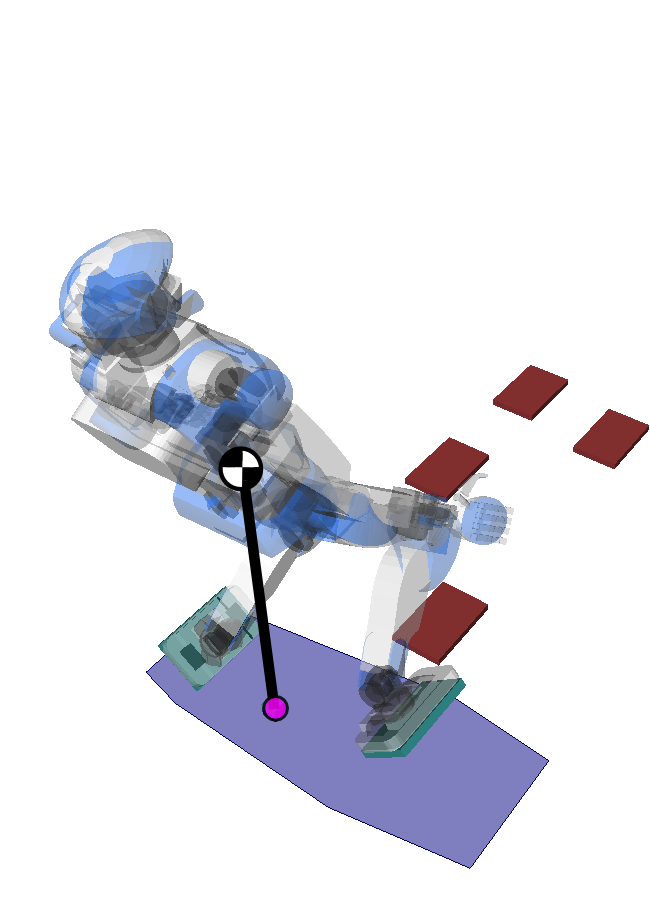
Pendular Support Area

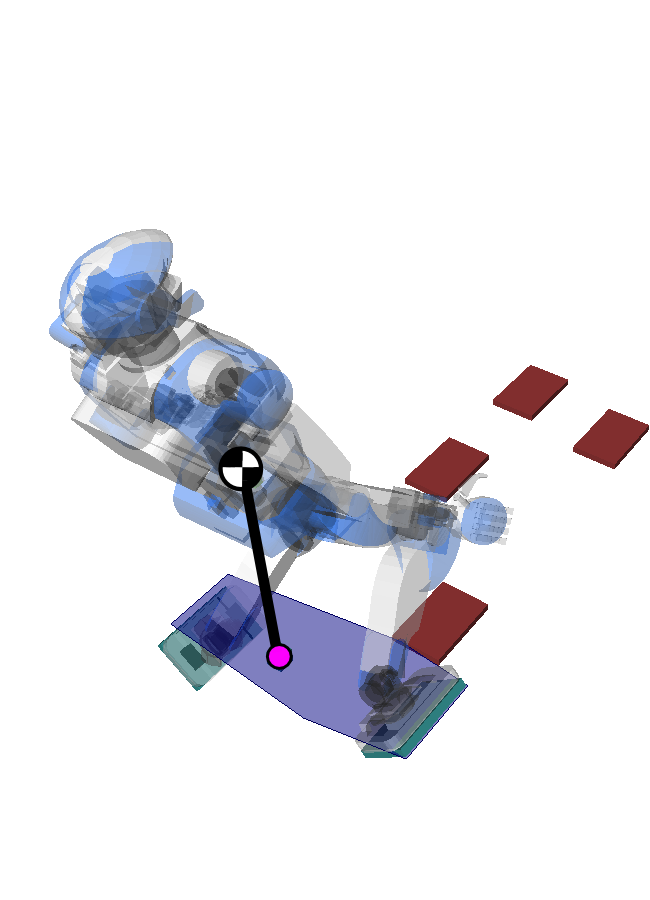
Pendular Support Area

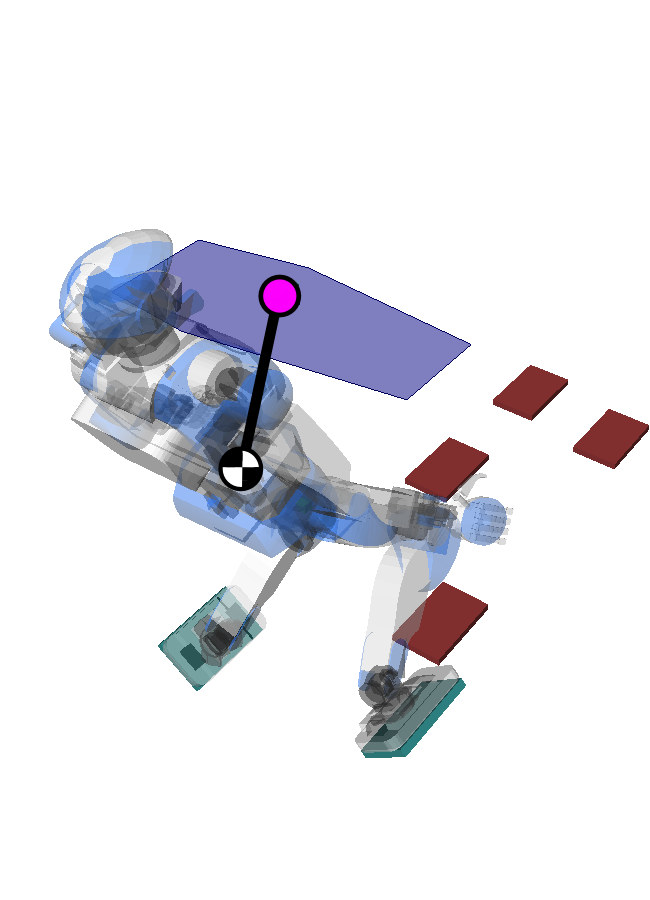
Pendular Support Area

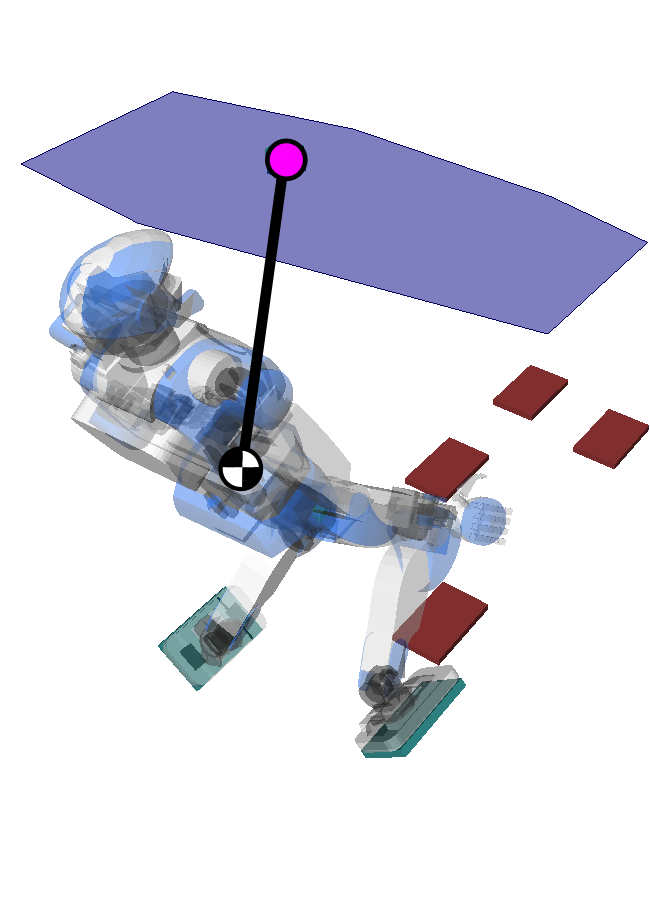
Linear Pendulum Mode

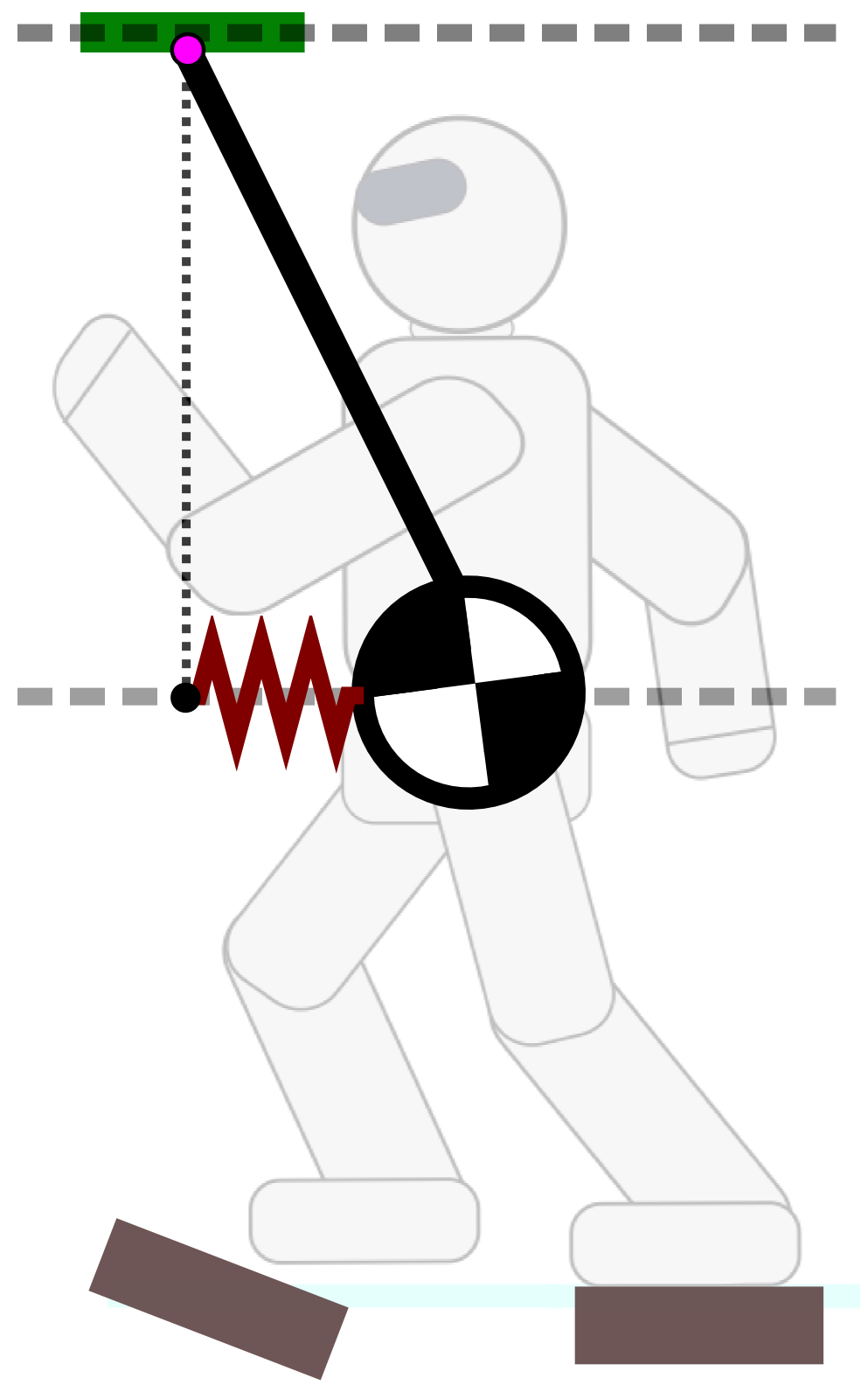
We can now consider the ZMP above the COM $\Rightarrow$ Linear (non-inverted) Pendulum Mode:

This is the dynamic equation of a spring.

Attractivity

• LIPM: the ZMP is a repellor of the COM
• LPM: the ZMP is a marginal attractor of the COM

The robot is driven from above, controlling its target position.

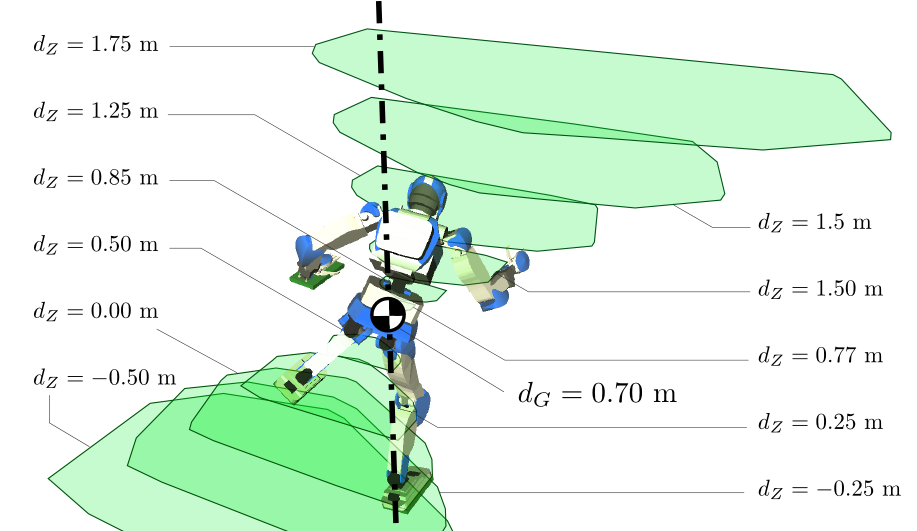
Observation

The shape of the pendular support area changes “conically” with the ZMP altitude: