ZMP support areas for
multi-contact locomotion



Stéphane Caron
LIRMM, CNRS-UM2
Work with Q.-C. Pham & Y. Nakamura
Journées Nationales de la Robotique Humanoïde
June 23, 2016
Walking on flat floors

- Start from a footstep plan
Walking on flat floors
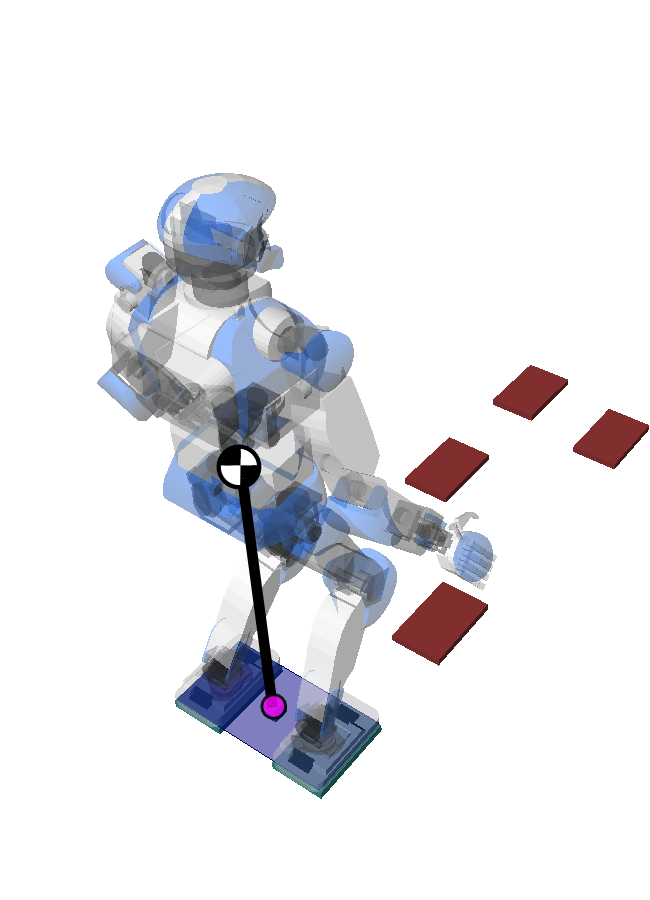
- Start from a footstep plan
- Regulate system dynamics around the Linear Inverted Pendulum Mode (LIPM)
Walking on flat floors
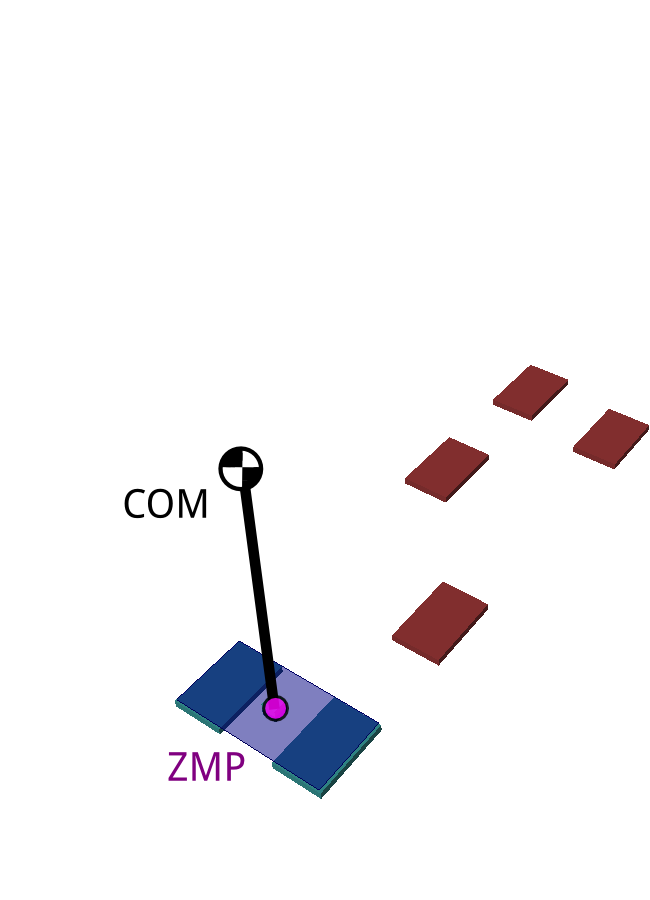
- Start from a footstep plan
- Regulate system dynamics around the Linear Inverted Pendulum Mode (LIPM)
- LIPM has simplified:
- Dynamics: ¨xG=ω2(xG−xZ)
- Contact stability criterion:
ZMP inside the support polygon
Walking on flat floors
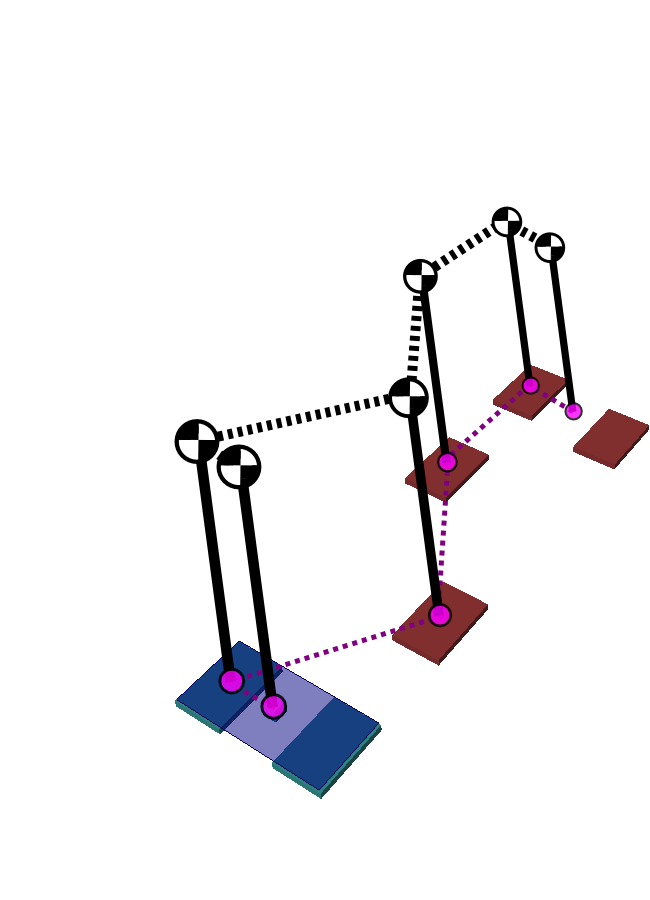
- Start from a footstep plan
- Regulate system dynamics around the Linear Inverted Pendulum Mode (LIPM)
- LIPM has simplified:
- Dynamics: ¨xG=ω2(xG−xZ)
- Contact stability criterion:
ZMP inside the support polygon
- Plan a trajectory for the pendulum
Walking on flat floors
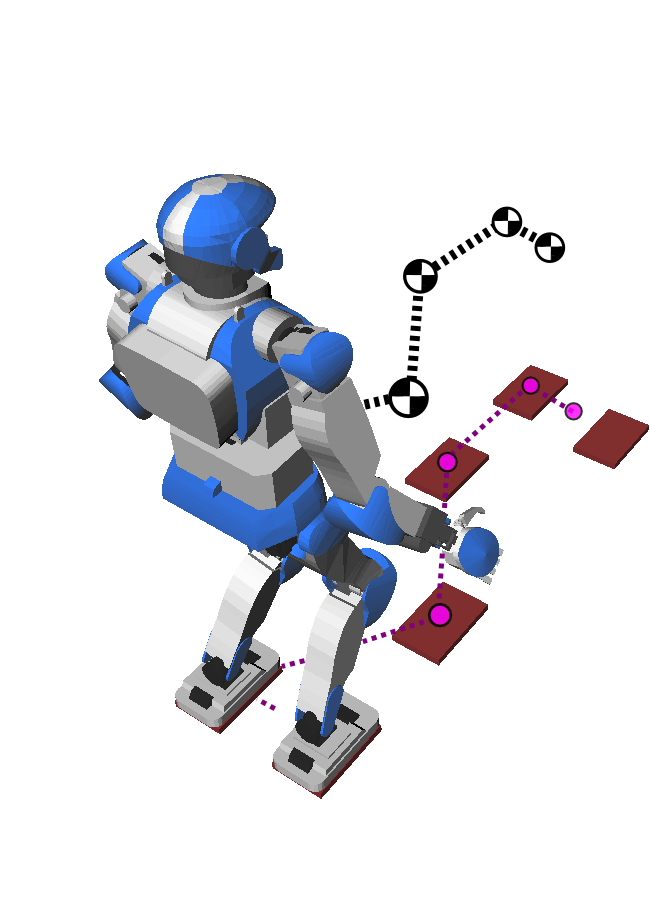
- Start from a footstep plan
- Regulate system dynamics around the Linear Inverted Pendulum Mode (LIPM)
- LIPM has simplified:
- Dynamics: ¨xG=ω2(xG−xZ)
- Contact stability criterion:
ZMP inside the support polygon
- Plan a trajectory for the pendulum
- Send it as reference to a whole-body controller
Question

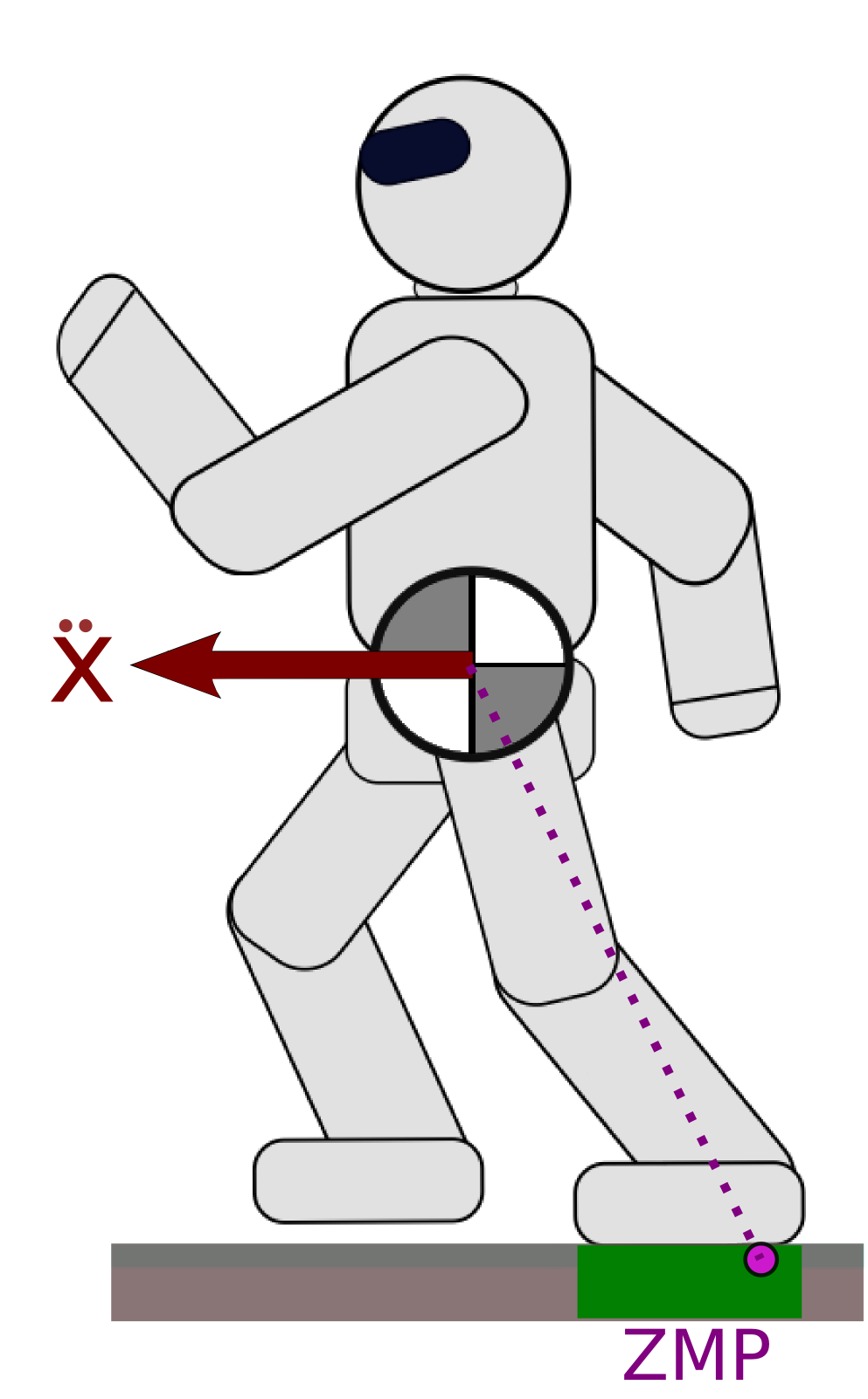
Zero-tilting Moment Point
Definition
The ZMP is traditionally defined as the point on the floor where the moment of the contact wrench is parallel to the surface normal (Sardain & Bessonnet, 2004).
Intuition
The point at which the robot “applies its weight”.
Contact stability
The ZMP must lie inside the support polygon (convex hull of ground contact points).1
Limitations
- This definition requires a single “floor” surface (no multi-contact)
- The support polygon does not account for frictional limits (slippage, yaw rotations).
Contact stability
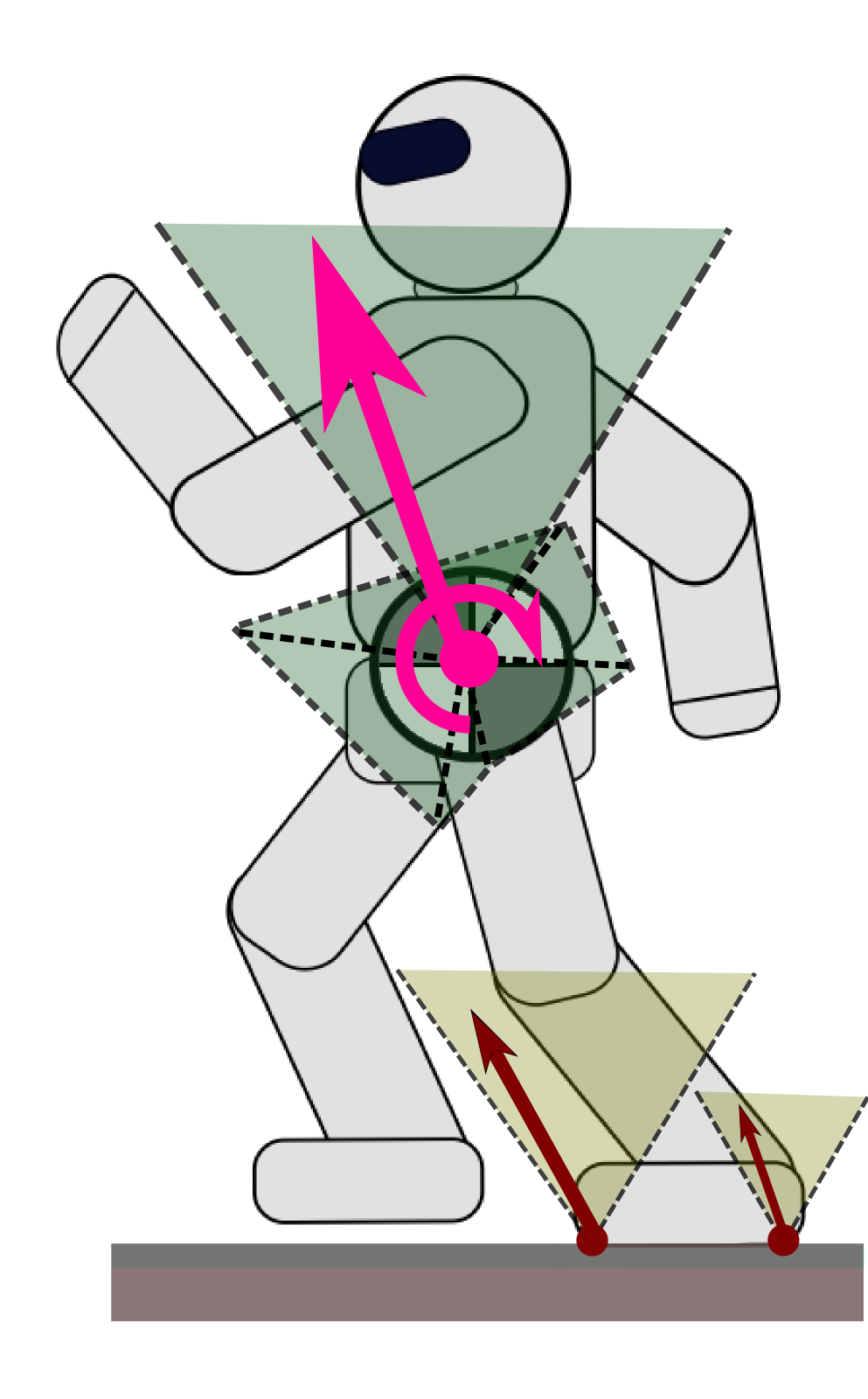
What wrenches are feasible under frictional contacts?
Weak Contact Stability
A motion or wrench is weak contact stable iff it can be realized by contact forces inside their friction cones.
Contact Wrench Cone
Friction cones can be combined as Contact Wrench Cone (CWC) at the
COM—see e.g. (Caron et al.,
2015).
By construction,
ZMP of a Wrench
The ZMP is mathematically defined from a wrench (Sardain & Bessonnet, 2004). The ZMP in the plane Π(O,n) of normal n containing O is the point such that n×τZ=0, that is:
xZ=n×τOn⋅f+xO.We define the full support area S as the image of the CWC by this equation.
Contribution 1
Good news! This area can be computed geometrically:
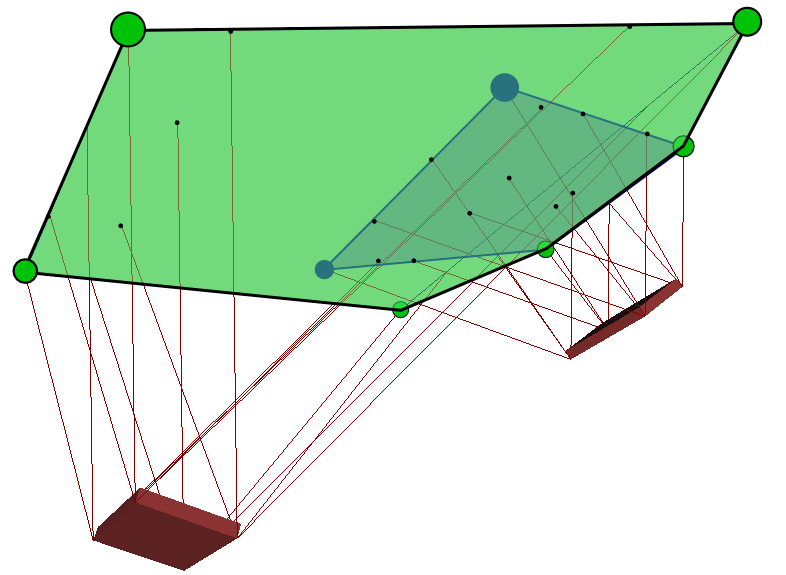
Contribution 1
Bad news! It is not always a polygon:
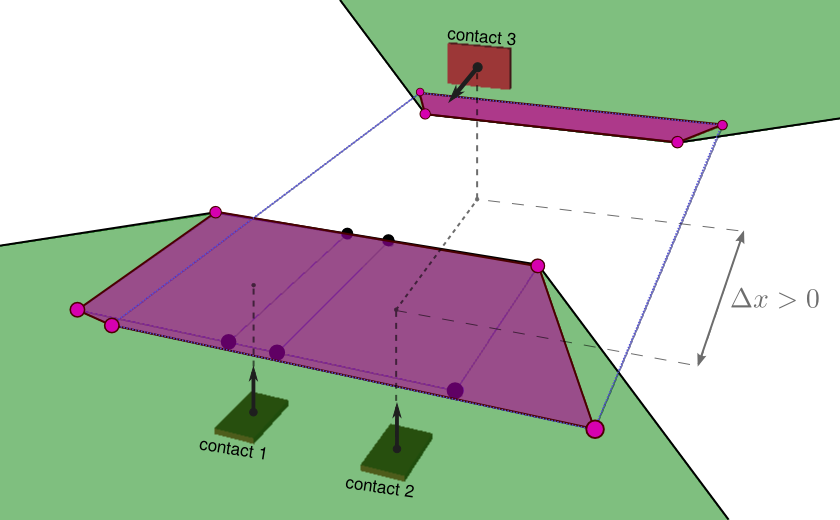
Centroidal dynamics

The Newton-Euler equations of the system are:
[m¨xG˙LG]=[mg0]+∑contacti[fi−−→GCi×fi]- m and g: total mass and gravity vector
- ¨xG: acceleration of the center of mass (COM)
- ˙LG: rate of change of the angular momentum
- fi: contact force received at contact point Ci
They show how the motion of unactuated DOFs results from interactions with the environment.
Linear Pendulum Mode
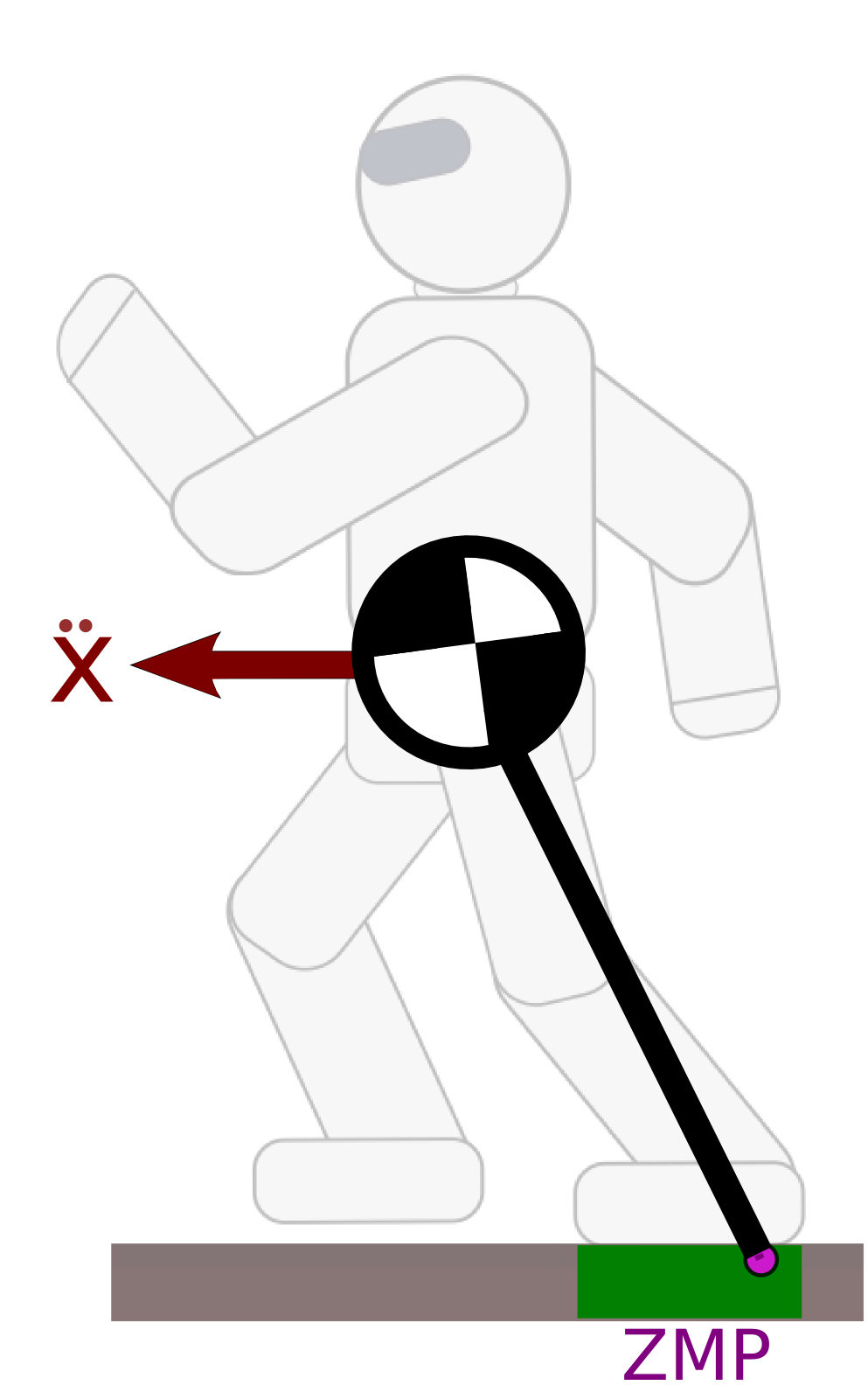
The Newton equation can be written equivalently:
¨xG=g+¨zGzG−zZ(xG−xZ)−˙LGxm(zG−zZ)where x now denotes X-Y plane coordinates. The Linear Inverted Pendulum Mode (Kajita et al., 2001) is obtained by constraining:
zG−zZ=h˙LG=0The system dynamics become ¨xG=gh(xZ−xG).
Observation
The support area in the LIPM is smaller than the convex hull of contact points:

Contribution 2
We provide an algorithm to compute the support area corresponding to the system:
w∈CWCzG−zZ=h˙LG=0We call it the pendular support area.
Pendular Support Area

Pendular Support Area

Pendular Support Area
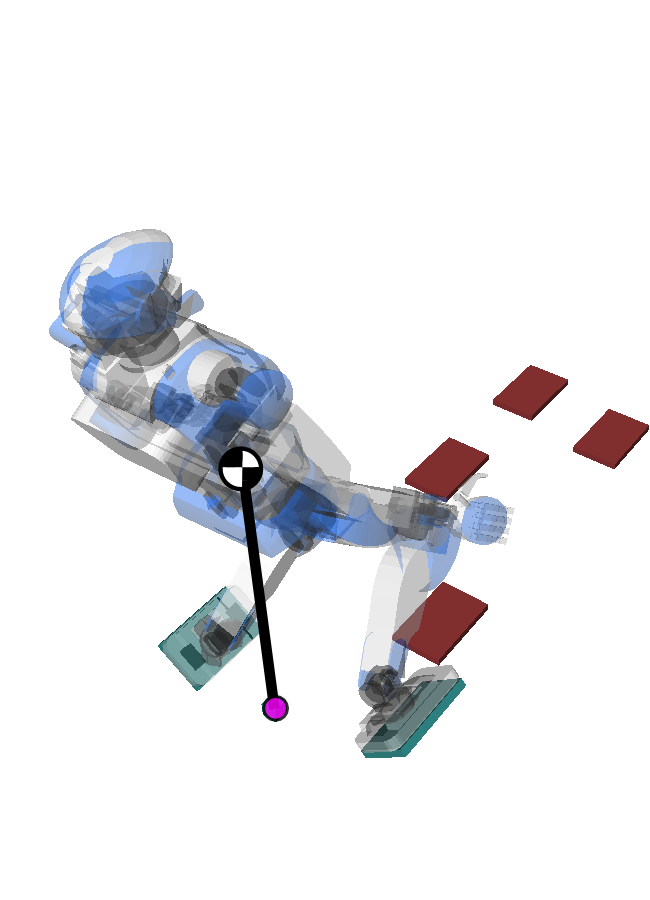
Pendular Support Area
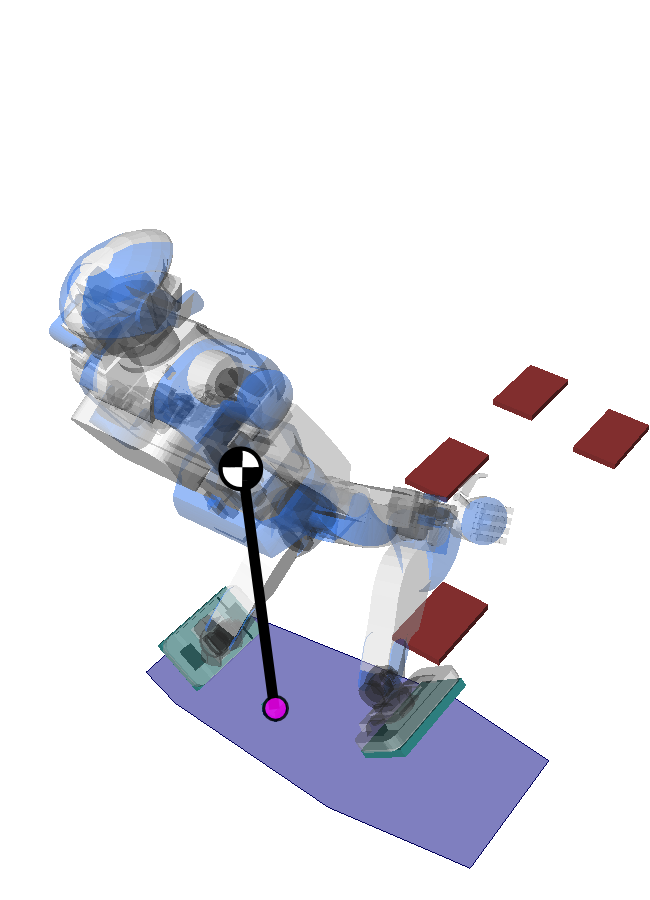
Pendular Support Area
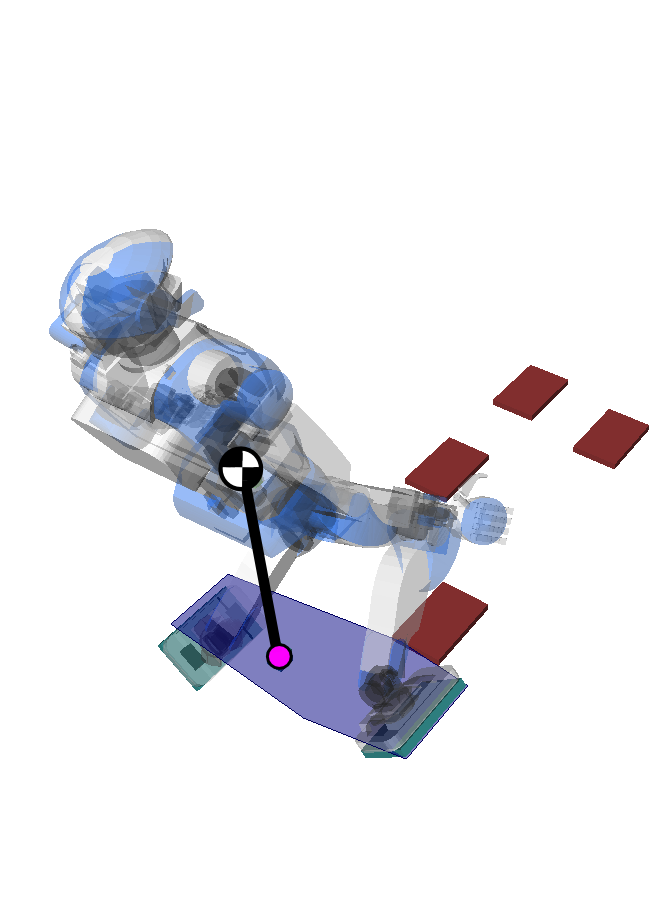
Pendular Support Area
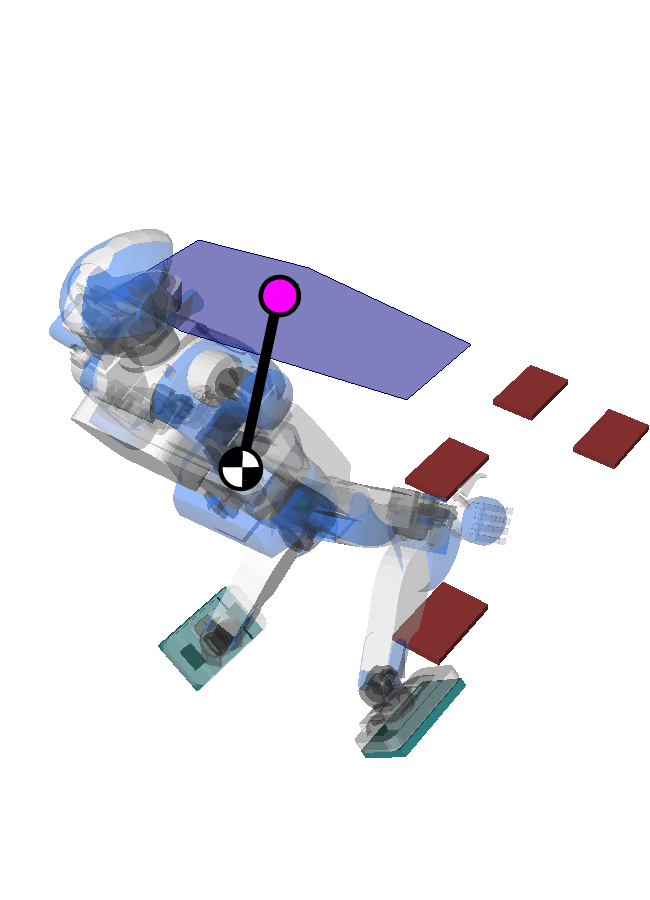
Pendular Support Area
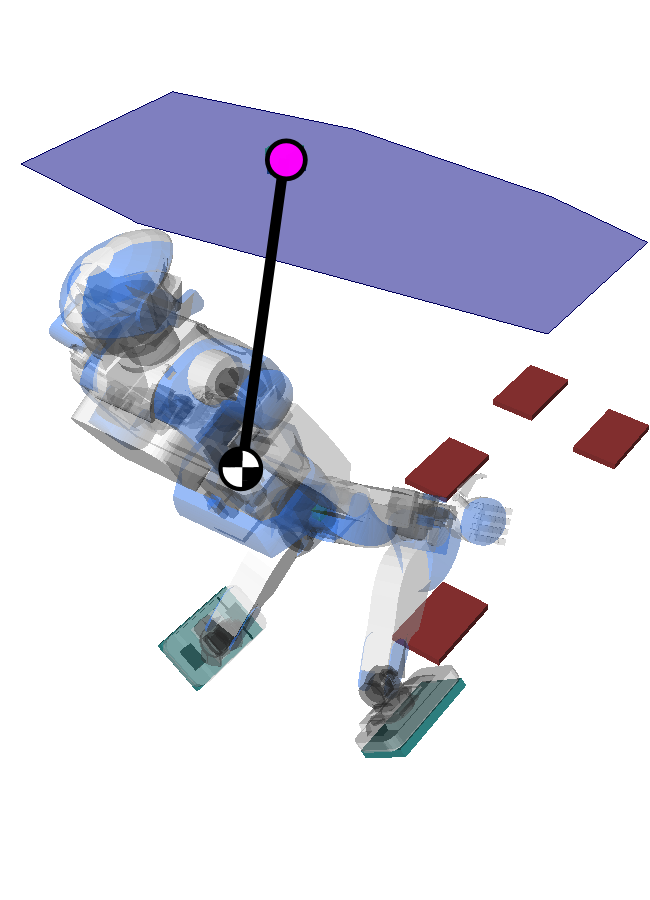
Linear Pendulum Mode
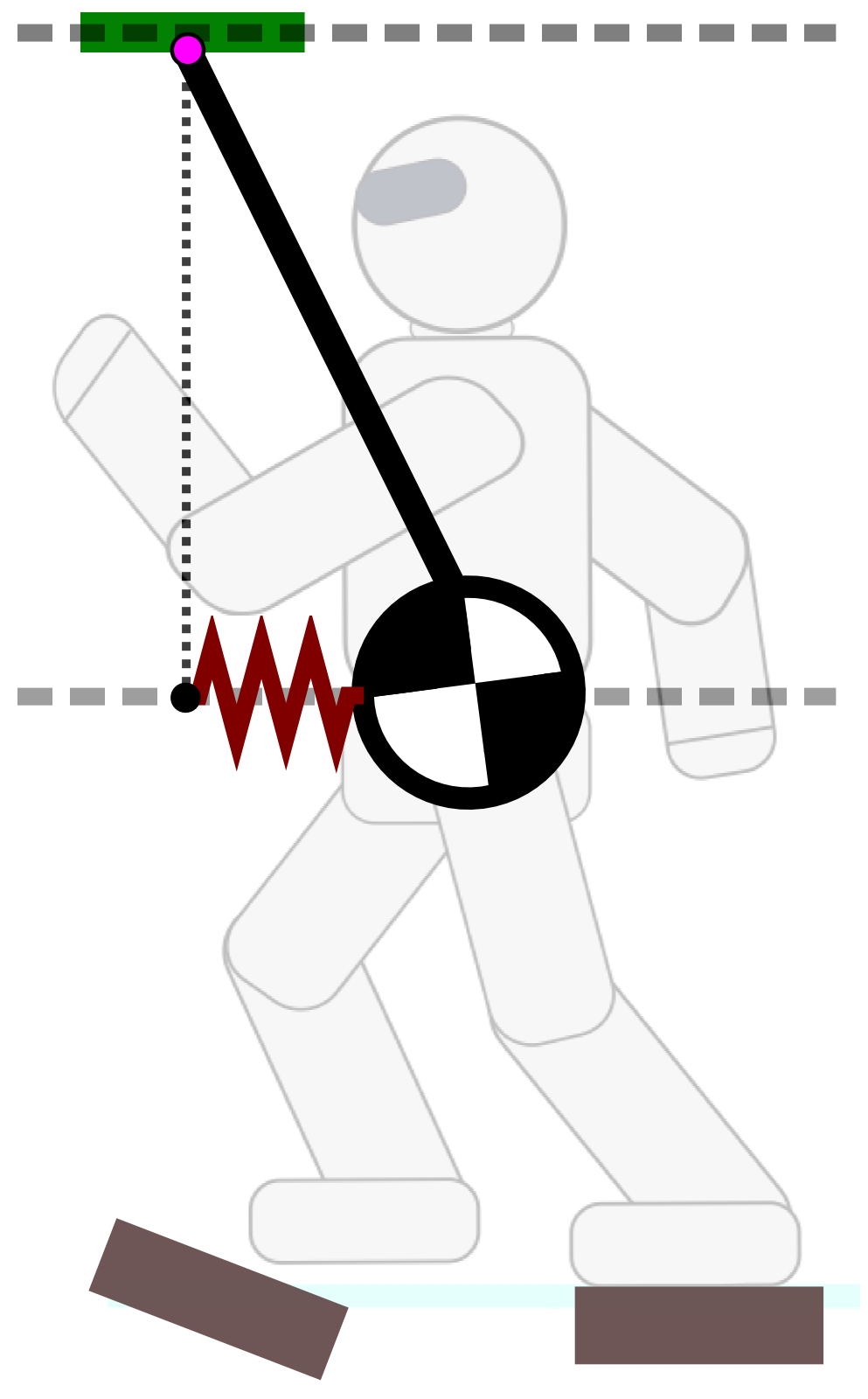
We can now consider the ZMP above the COM ⇒ Linear (non-inverted) Pendulum Mode:
¨xG = gh(xG−xZ)This is the dynamic equation of a spring.
Attractivity
- LIPM: the ZMP is a repellor of the COM
- LPM: the ZMP is a marginal attractor of the COM
The robot is driven from above, controlling its target position.
Observation
The shape of the pendular support area changes “conically” with the ZMP altitude:
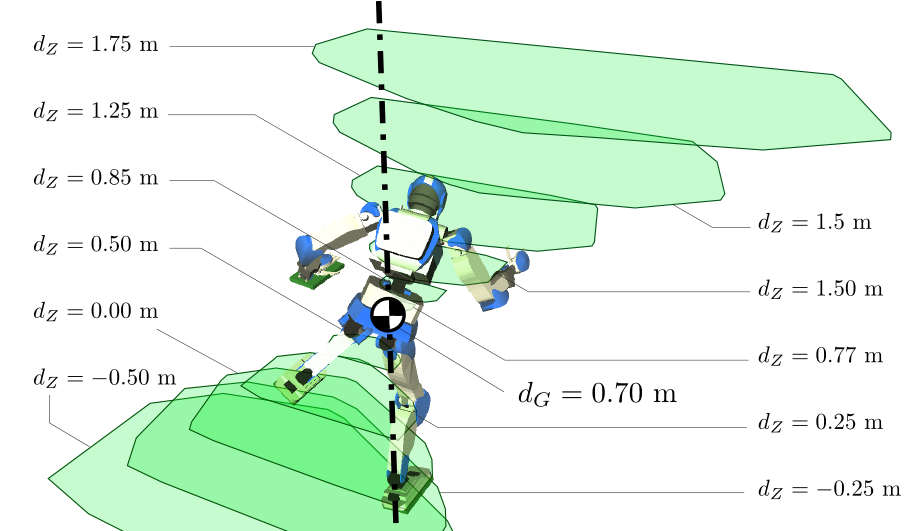
Conclusion
- Geometric construction of general ZMP support areas
- Linear-pendulum mode for multi-contact locomotion


Merci pour votre attention.
