Physical contacts can be modeled as degrees of constraints that mobile robots
maintain while moving. They stem from the non-penetrability condition: if
dij is the distance between the closest pair of points, one
belonging to a body i and the other to a body j=i, then
dij≥0.When dij>0, there is no contact and the two bodies may move
freely. But as soon as dij=0, contact appears and constraints the
respective motions of the two bodies.
Definition from degrees of constraints
In rigid body dynamics, a body has six degrees of freedom, three for its
translation and three for its orientation. Therefore, a contact can create
between one and six degrees of constraints (DOC), depending on the number and
arrangement of contact points between the contacting bodies.
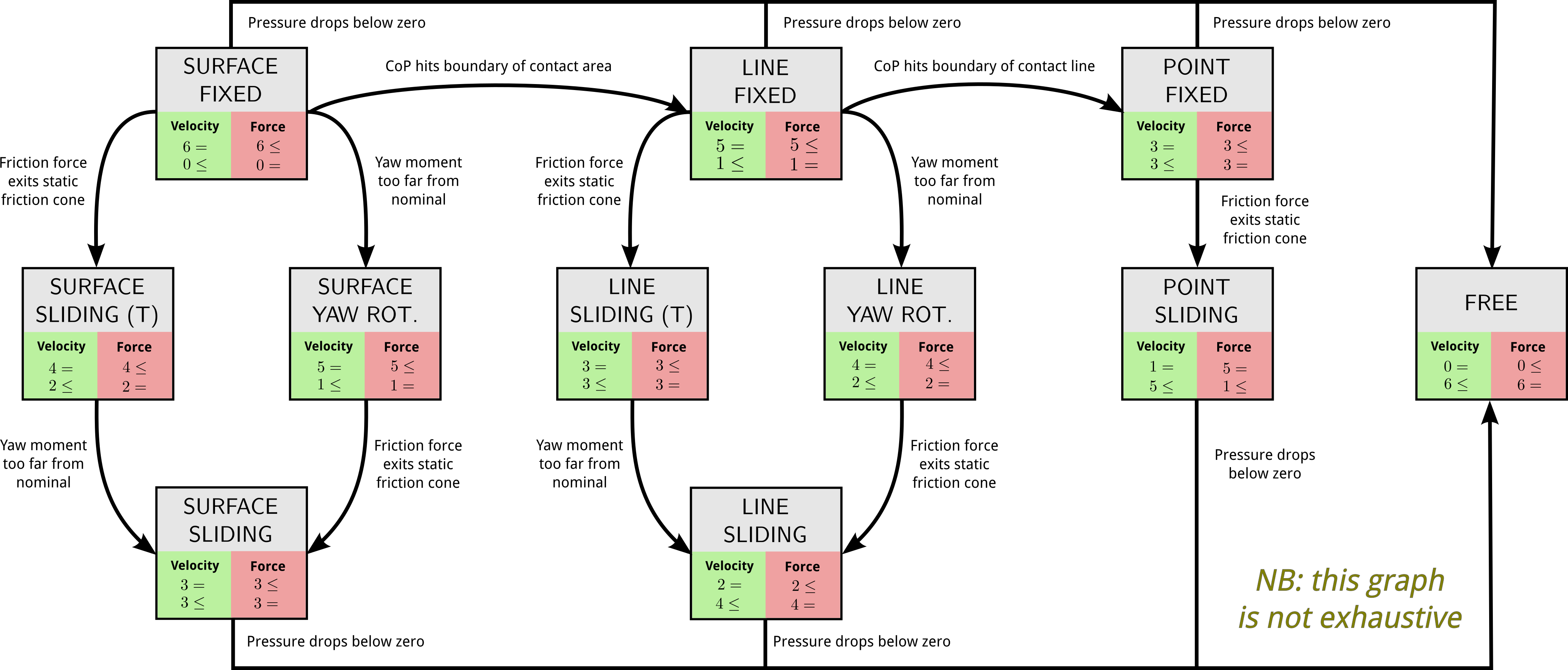
- Definition (Balkcom and Trinkle):
- The mode of a contact is the set of degrees of constraints that it
introduces between the two contacting bodies.
Common contact modes include:
- Broken: When there is no contact (DOC: 0)
- Sliding: When there is a relative translation between contact surfaces,
accompanied or not by a rotation along the contact normal (DOC: 3 or 4)
- Rolling: When one body in contact is rotating around a line on the other
body, accompanied or not by a translation along that line (DOC: 2 or 3)
- Fixed: When the contact is fully constrained (DOC: 6)
To go further
The article by Balkcom and Trinkle (2002) introduced several important
ideas, including contact modes and the representation of contact conditions by
polyhedral convex sets.
Discussion
Feel free to post a comment by e-mail using the form below. Your e-mail address will not be disclosed.