The Jacobian-transpose term maps external contact forces to joint torques (for
actuated coordinates) and to the net floating-base wrench (for unactuated
coordinates). We will see how to derive it from the principle of least
constraint, using the method of Lagrange multipliers.
Constraint derivatives
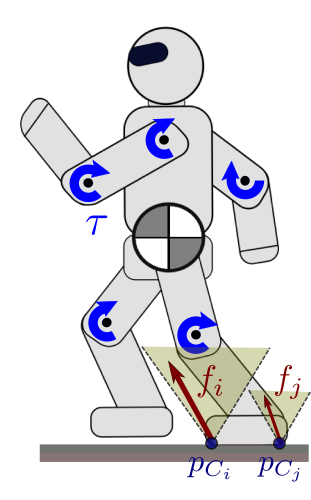
We consider a legged robot, for example the humanoid depicted in the figure to
the right, making point contacts or
surface contacts
with its environment. These kinematic constraints can be summarized into a
holonomic constraint
c(q)=0. In the case of point contacts, it would be the
stack of contact point equality constraints pC(q)=pD,
with pC the mobile point on the robot's foot and pD the
ground contact point in the inertial frame. Differentiating c(q)=0 twice with respect to time yields:
Jc(q)q¨+q˙⊤Hc(q)q˙=0where the constraint Jacobian and Hessian matrices are defined by:
Jc(q)=∂q∂c(q)Hc(q)=∂q2∂2c(q)The Jacobian is a 3k×n matrix, with k the number of
contact poins and with n the degree of freedom of our robot (number of
actuated joints plus six), while the Hessian is an n×3k×n tensor. Notations are the same for surface contacts, except that the degree
of constraint for each contact is six rather than three.
Principle of least constraint
Remember how, in the absence of constraint, the equations of free motion of
our system would be:
M(q)q¨free+q˙⊤C(q)q˙=S⊤τ+τg(q)+τextwhere:
- M(q) is the n×n joint-space inertia matrix,
- C(q) is the n×n×n joint-space Coriolis tensor,
- τ is the n-dimensional vector of actuated joint torques,
- τg(q) is the n-dimensional vector of gravity torques,
- τext is an optional vector of external forces and torques.
We know how to compute these matrices and
vectors from
link inertias and Jacobians. However, when the robot is in contact, its motion
doesn't follow the vector q¨free defined by this equation
because of the additional contact constraint: the actual q¨ has to be
such that
Jc(q)q¨+q˙⊤Hc(q)q˙=0Gauss's principle of least constraint
states that the robot's actual acceleration q¨ is as close as
possible to the free acceleration q¨free, subject to
this constraint:
q¨=argminasubject to21∥a−q¨free∥M2Jc(q)a+q˙⊤Hc(q)q˙=0Note how the inertia matrix appears in the objective function to define what
as close as possible means here. The inertia matrix is positive definite so
this objective function is strictly convex.
Method of Lagrange multipliers
From the method of Lagrange multipliers, the optimum
(a∗,λ∗) of our constrained problem is a critical point of
the Lagrange function:
∂a∂L(a∗,λ∗)=0∧∂λ∂L(a∗,λ∗)=0The second equation is, by construction, our contact constraint. The first one
gives us:
M(a∗−q¨free)−JcTλ∗=0In fine, replacing a∗ by our notation for joint accelerations
q¨ and similarly λ∗ by f, we obtain the
constrained equations of motion in joint space:
M(q)q¨+q˙⊤C(q)q˙=S⊤τ+τg(q)+τext+Jc⊤fwith M(q) the joint-space inertia matrix, C(q) the
joint-space Coriolis tensor, τg(q) the vector of gravity
torques, τ the vector of actuated joint torques, Jc the
stacked Jacobian of kinematic contact constraints and f the
corresponding stacked vector of contact forces.
To go further
This page is based on Wieber's comments on the structure of the dynamics of
articulated motion, as well as
on a very good summary in Section IV.A of this paper by Budhiraja et al.
Forces are virtual quantities that balance out our calculations. Defining them
as the dual multipliers of motion constraints is a key step in Lagrangian
mechanics: constraints "pull" on the system, which aspires to be somewhere else
according to the principle of least motion, and multipliers can be seen as a
measure of how hard the constraints need to pull to keep the system on track.
Check out Jensen's explanation on the meaning of the multiplier for
some great examples to build up intuition around this.
